STRUCTURAL DESIGN APPS

Guest

Guest User
Login
SignUp

母屋の設計

データ名：---
プロジェクト名：---
更新日：---
Proにアップグレードすれば全ての機能が使えます!
コピー元のデータを選択してください。
削除するデータを選択してください。

基本事項

荷重入力

積載荷重

風荷重

積雪荷重

クライテリア

・長期

・短期

断面性能

ft(長期) =N/㎟

ft(短期) =N/㎟

fb(長期) =N/㎟

fb(短期) =N/㎟


qa(長期) =kN/本

qa(短期) =kN/本

Ta(長期) =kN/本

Ta(短期) =kN/本


Ix =cm4

IY =cm4

Zx =cm3

Zy =cm3

A =cm2


iy =cm

J =cm4

λy =

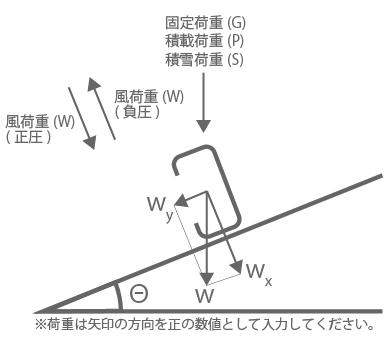
W =N/m

荷重組合わせ

力の
種類		想定する
状態		荷重組合わせw(N/m)wx(N/m)wy(N/m)
長期 常時 G + P
短期 暴風時 G + P + W(正圧)
G + P + W(負圧)
積雪時 G + P + S

G : 固定荷重、P : 積載荷重、W : 風荷重、S : 積雪荷重

曲げ

・常時 :

Mx = kNm My = kNm

σbx = N/㎟ σby = N/㎟

→σbx/fb + σbx/ft =

・風荷重時 :

(正圧)

Mx = kNm My = kNm

σbx = N/㎟ σby = N/㎟

→σbx/fb + σbx/ft =

(負圧)

Mx = kNm My = kNm

σbx = N/㎟ σby = N/㎟

→σbx/fb + σbx/ft =

・積雪時 :

(長期)

Mx = kNm My = kNm

σbx = N/㎟ σby = N/㎟

→σbx/fb + σbx/ft =

(短期)

Mx = kNm My = kNm

σbx = N/㎟ σby = N/㎟

→σbx/fb + σbx/ft =

せん断

・常時 :

Qx = kN Qy = kN

→ √((Qx/Qa)2 + (Qy/Ta)2) =

・風荷重時 :

(正圧)

Qx = kN Qy = kN

→ √((Qx/Qa)2 + (Qy/Ta)2) =

(負圧)

Qx = kN Qy = kN

→ √((Qx/Qa)2 + (Qy/Ta)2) =

・積雪時 :

(長期)

Qx = kN Qy = kN

→ √((Qx/Qa)2 + (Qy/Ta)2) =

(短期)

Qx = kN Qy = kN

→ √((Qx/Qa)2 + (Qy/Ta)2) =

たわみ

・常時 :

δx =㎜ δy =㎜

→ δ(= √(δx2+δy2) ) =㎜ ( δ/l = )

・風荷重時 :

(正圧)

δx =㎜ δy =㎜

→ δ(= √(δx2+δy2) ) =㎜ ( δ/l = )

(負圧)

δx =㎜ δy =㎜

→ δ(= √(δx2+δy2) ) =㎜ ( δ/l = )

・積雪時 :

(長期)

δx =㎜ δy =㎜

→ δ(= √(δx2+δy2) ) =㎜ ( δ/l = )

(短期)

δx =㎜ δy =㎜

→ δ(= √(δx2+δy2) ) =㎜ ( δ/l = )

母屋選定図

  • ～

解説

  • 入力内容の解説
  • 計算内容の解説
  • 規基準
  • 参考文献
梁種別 : 単純梁と2連梁から選択します
l : 下図によります。
母屋ピッチ : 母屋の間隔を指定します。
母屋勾配 : 屋根の勾配を０～９０°の範囲で指定します。
lb : 座屈長さ(m)、0にすると横座屈を考慮しません。
断面種別 : リップ溝形鋼,角形鋼管から選択できます。
断面 : 各種断面寸法の入力値は下記によります。
端部ボルト : 本数、径、種別、接合条件(1面せん断 or 2面せん断)を指定します。

許容曲げ応力度fbの計算

a)リップ溝型鋼

鋼構造許容応力度設計規準の方法によります。本アプリではpλb=0.3、C=1.0で計算しています。

λb≧pλbのとき

\[ f_{b} = \frac{F}{ν} \]

pλb<λb≦eλbのとき

\[ f_{b} = \frac{\left\{1 - 0.4\frac{λ_{b}ー_{p}λ_{b}}{_{e}λ_{b} - _{p}λ_{b}}\right\}F}{ν} \]

eλb<λbのとき

\[ f_{b} = \frac{1}{λ^{2}_{b}}・\frac{F}{2.17} \]

ここに

\[ λ_{b} = \sqrt{\frac{M_{y}}{M_{e}}} \] \[ M_{e} = C\sqrt{\frac{π^{4}EI_{Y}・EI_{w}}{l_{b}^{4}}+\frac{π^{2}EI_{Y}・GJ}{l^{2}_{b}}} \] \[ _{p}λ_{b} = \frac{1}{\sqrt{0.6}} \]

i) 補剛区間内で曲げモーメントが単調に変化する場合

\[ _{p}λ_{b} = 0.6 + (\frac{M_{2}}{M_{1}}) \] \[ C = 1.75 + 1.05(\frac{M_{2}}{M_{1}}) + 0.3(\frac{M_{2}}{M_{1}})^{2} ≦ 2.3 \]

ii) 補剛区間内で曲げモーメントが単調に変化する場合

\[ _{p}λ_{b} = 0.3 \] \[ C = 1.0 \]

記号

fb : 許容曲げ応力度
λb : Myに対する曲げ材の基準化細長比
lb : 圧縮フランジの支点間距離
ν : 安全率(ν = 3/2 + (2/3)(λb/eλb)2)
eλb : 弾性限界細長比
pλb : 塑性限界細長比
Me : 弾性横座屈モーメント
My : 降伏モーメント(My=F・Z)
Z : 断面係数
C : 弾性横座屈モーメントの補正係数
IY : 弱軸まわりの断面二次モーメント
Iw : 曲げねじり定数
G : せん断弾性係数
J : サンブナンのねじり定数
M1、M2 : それぞれ座屈補剛区間の両端に作用する大きいほう、小さいほうの、橋軸まわりの曲げモーメント。 M2/M1は複曲率の場合は正、単曲率の場合は負となる。

b)角形鋼管

許容曲げ応力度fbはftとします。

高力ボルト・ボルトの許容応力

高力ボルト及び、ボルトの許容せん断耐力は下記によります。

高力ボルトの許容せん断耐力
高力ボルトの鋼種 ボルト呼び径 設計用張力T0 許容せん断力(kN/本)
長期短期
許容せん断力
1面摩擦2面摩擦
F8T(溶融亜鉛めっきボルト)M1245.812.124.1長期の1.5倍
M1685.221.442.9
M2013333.567.0
M2216540.581.1
M2419248.296.4
M2725061.0122.0
M3030575.4151.0
F10TM1256.917.033.9
M1610630.260.3
M2016547.194.2
M2220557.0114.0
M2423867.9136.0
M2731085.9172.0
M30379106.0212.0
ボルトの許容せん断耐力
強度区分 ボルト呼び径 許容耐力(kN/本)
長期短期
せん断力許容引張力
1面せん断2面せん断
4.6、4.8M127.7915.613.5長期の1.5倍
M1614.529.025.1
M2022.645.339.2
M2228.056.048.5
M2432.665.256.5
M2742.484.873.4
M3051.810489.8
5.6、5.8M129.7319.516.9
M1618、136.331.4
M2028.356.649.0
M2235.070.060.6
M2440.881.570.6
M2753.0106.091.8
M3064.8130.0112
6.8M1213.627.323.6
M1625.450.844.0
M2039.679.268.6
M2249.098.084.8
M2457.1114.098.9
M2774.2148.0129
M3090.7181.0157

引張力を受けるボルト・高力ボルトの許容応力

引張力を受ける高力ボルト及び、普通ボルトの許容せん断耐力は下記によります。

a)高力ボルト

参考文献１より引張力を受ける高力ボルトの許容せん断力は下記によります。

fst = fs0(1 - σt・A/T0)

ここで、

fst : 引張力を同時に受ける高力ボルトの許容せん断力
fs0 : 上表に示す高力ボルトの許容せん断力
σt : ボルトに加わる引張応力度
T0 :上表に示す設計用 ボルト張力
A : 高力ボルトの軸断面積

fstをQx、σt・AをQaとして上式を変換すると下記のようになります。

Qx < Qa(1 - Qy/T0)

→ Qx/Qa + Qy/T0 < 1

ここで、

Qx : ボルトの設計用せん断力
Qy : ボルト引張方向のせん断力
Qa : ボルトの許容せん断力

b)中ボルト

引張力を受けるボルトの許容せん断力は下記によります。

√((Qx/Qa)2 + (Qy/Ta)2) < 1

ここで、

Ta : 上表に示すボルトの許容引張力
その他は前出による

曲げ応力度の計算

母屋の最大曲げ応力度は下記によります。

σbmax = Mx/zx + My/zy

ここで、

σbmax : 母屋の最大曲げ応力度
Zx : 強軸の断面係数
Zy : 弱軸の断面係数
Mx : 強軸方向最大曲げ応力で下記によります
Mx = (W*l2/8)*cosΘ
My : 弱軸方向最大曲げ応力で下記によります
My = (W*l2/8)*sinΘ
l : 部材長
w : 図1によります。
Θ : 図1によります。

せん断応力の計算

母屋の最大せん断力は下記によります。

a)単純梁

Qx = wx*l/2

Qy = wy*l/2

b)2連梁

Qx = 5*wx*l/4

Qy = 5*wy*l/4

ここで、

Qx : x方向最大せん断力
Qy : y方向最大せん断力
w : 図1によります。
wx : w*cosΘ
wy : w*sinΘ
l : 部材長

たわみの計算

母屋の最大たわみは下記により計算します。

δmax = √(δx2 + δy2)

ここで、

δx : x方向最大たわみで以下によります

a)単純梁

δx = wx*l4/(384*E*Ix)

b)2連梁

δx = wx*l4/(185*E*Ix)
δy : y方向最大たわみで以下によります

a)単純梁

δy = wy*l4/(384*E*Iy)

b)2連梁

δy = wy*l4/(185*E*Iy)
w : 図1によります。
wx : w*cosΘ
wy : w*sinΘ
l : 部材長
E : ヤング係数
Ix : 強軸方向の断面二次モーメント
Iy : 弱軸方向の断面二次モーメント

図1 母屋荷重図

（保有水平耐力計算）

第82条

前条第二項第一号イに規定する保有水平耐力計算とは、次の各号及び次条から第八十二条の四までに定めるところによりする構造計算をいう。
一 第二款に規定する荷重及び外力によつて建築物の構造耐力上主要な部分に生ずる力を国土交通大臣が定める方法により計算すること。
二 前号の構造耐力上主要な部分の断面に生ずる長期及び短期の各応力度を次の表に掲げる式によつて計算すること。
力の種類 荷重及び外力について想定する状態 一般の場合 第八十六条第二項ただし書の規定により特定行政庁が指定する多雪区域における場合 備考
長期に生ずる力 常時 Ｇ＋Ｐ Ｇ＋Ｐ 　
積雪時 Ｇ＋Ｐ＋０．７Ｓ
短期に生ずる力 積雪時 Ｇ＋Ｐ＋Ｓ Ｇ＋Ｐ＋Ｓ 　
暴風時 Ｇ＋Ｐ＋Ｗ Ｇ＋Ｐ＋Ｗ 建築物の転倒、柱の引抜き等を検討する場合においては、Ｐについては、建築物の実況に応じて積載荷重を減らした数値によるものとする。
Ｇ＋Ｐ＋０．３５Ｓ＋Ｗ
地震時 Ｇ＋Ｐ＋Ｋ Ｇ＋Ｐ＋０．３５Ｓ＋Ｋ 　
この表において、Ｇ、Ｐ、Ｓ、Ｗ及びＫは、それぞれ次の力（軸方向力、曲げモーメント、せん断力等をいう。）を表すものとする。 Ｇ　第八十四条に規定する固定荷重によつて生ずる力 Ｐ　第八十五条に規定する積載荷重によつて生ずる力 Ｓ　第八十六条に規定する積雪荷重によつて生ずる力 Ｗ　第八十七条に規定する風圧力によつて生ずる力 Ｋ　第八十八条に規定する地震力によつて生ずる力
三 第一号の構造耐力上主要な部分ごとに、前号の規定によつて計算した長期及び短期の各応力度が、それぞれ第三款の規定による長期に生ずる力又は短期に生ずる力に対する各許容応力度を超えないことを確かめること。
四 国土交通大臣が定める場合においては、構造耐力上主要な部分である構造部材の変形又は振動によつて建築物の使用上の支障が起こらないことを国土交通大臣が定める方法によつて確かめること。

1) (社)日本建築学会、鋼構造許容応力度設計基準、2019.10

2) 全国官報販売協同組合、2020年版 建築物構造関係技術基準解説書、2022.11