1.接地圧の検討
接地圧の検討では、柱軸力、付加曲げ応力、基礎自重、基礎上部の土の重量を考慮した最大の接地圧が許容地耐力未満であることを確認します。
1.1 偏心距離の計算
曲げ応力を考慮した鉛直荷重の偏心距離は式(1.1)により計算します。
\[
e = ε + e' ・・・・(1.1)
\]
記号
| e | : 接地圧検討用の偏心距離 |
| ε | : 柱心と基礎心の偏心距離 |
| e' | : 曲げ応力による偏心距離(=M/N) |
| M | : 基礎付加曲げ応力 |
| N | : 柱軸力＋基礎自重＋基礎上部の土の自重 |
| N = N0 + Wf + Ws |
| N0 | : 柱軸力 |
| Wf | : 基礎自重 |
| WS | : 基礎上部の土の重量、D1+D2>Dfの場合は0 |
図1.1 基礎応力と偏心距離
1.2 接地圧の計算
最大、最小の接地圧の計算は下式によります。
\[
σ_{max} = (1 + _{x}α + _{y}α)\frac{N}{A} ・・・・(2.1)
\]
xe/L
x≦1/6かつ
ye/L
y≦1/6の時
\[
σ_{min} = (1 + _{x}α' + _{y}α')\frac{N}{A} ・・・・(2.2)
\]
xe/L
x1/6又は
ye/L
y>1/6の時
\[
σ_{min} = 0 ・・・・(2.3)
\]
記号
| σmax | : 最大接地圧 |
| σmin | : 最小接地圧 |
| A | : 基礎底面積 |
| Lx | : x方向の基礎幅 |
| Ly | : y方向の基礎幅 |
| xe | : x方向偏心距離 |
| ye | : y方向偏心距離 |
| xα、yα、xα'、yα' | : x,y方向偏心距離eによる圧縮応力度の係数。(下式) |
|
i) e/L ≦ 1/6の時
\[
α = 6*\frac{e}{l} ・・・・(3.1)
\]
\[
α' = -6*\frac{e}{l} ・・・・(3.2)
\]
ii) e/L > 1/3の時
\[
α = \frac{2}{3(\frac{1}{2}+\frac{e}{l})}-1 ・・・・(3.3)
\]
\[
α':なし、σ_{min}=0
\]
※e/L > 0.3となる場合は計算不可
|
| その他の記号は前出による |
2.基礎の設計
2.1 応力の計算
(1) 基礎設計用地反力の計算では、柱軸力のみを考慮し、基礎自重、基礎上部の土の重量を無視します。最大・最小地反力は式(2.1)～(2.3)によります。
(X方向の最大地反力計算)
\[
_{x}σ_{0max} = (1 + _{x}α_{0})\frac{N_{0}}{A} ・・・・(2.1)
\]
xe/L
x≦1/6の時
\[
_{x}σ_{0min} = (1 + _{x}α_{0}')\frac{N_{0}}{A} ・・・・(2.2)
\]
xe/L
x1/6又は
ye/L
y>1/6の時
\[
_{x}σ_{0min} = 0 ・・・・(2.3)
\]
記号
| xσmax | : x方向最大地反力 |
| xσmin | : x方向最小地反力 |
| Lx | : x方向の基礎幅 |
| xα、xα' | : x方向偏心距離eによる圧縮応力度の係数。(2.4)～(2.7)式 |
|
i) xe0/Lx ≦ 1/6の時
\[
_{x}α_{0} = 6*\frac{_{x}e_{0}}{L_{x}} ・・・・(2.4)
\]
\[
_{x}α'_{0} = -6*\frac{_{x}e_{0}}{L_{x}} ・・・・(2.5)
\]
ii) xe0/Lx > 1/6の時
\[
_{x}α_{0} = \frac{2}{3(\frac{1}{2}+\frac{_{x}e_{0}}{L_{x}})}-1 ・・・・(2.6)
\]
\[
_{x}α'_{0}:なし、σ_{min}=0・・・・(2.7)
\]
※xe0/Lx > 0.3となる場合は計算不可
|
| xe0 | : x方向偏心距離(=εx+e'0)〔図2.1参照〕による。 |
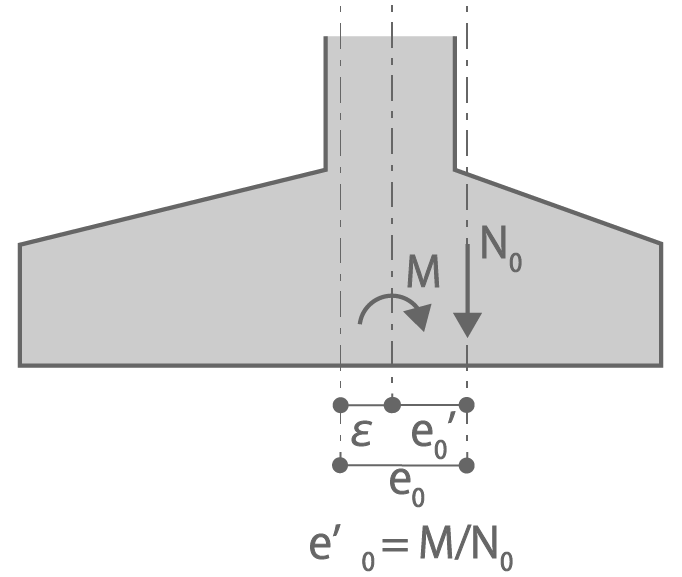|  図2.1荷重と偏心距離の関係 |
Y方向の地反力は(2.1)～(2.2)式のXをYに読み替える
(2) 基礎設計用の曲げ応力の計算は式(2.8)による。応力算定位置は〔図2.2〕参照
(X方向の最大曲げ応力の計算)
\[
_{x}M_{F} = N_{0}\frac{(1+_{x}α_{0})}{8}(1 - \frac{1}{6}\frac{L_{x}-a_{x}}{_{x}x_{n}})\frac{(L_{x}-a_{x})^{2}}{L_{x}}・・・・(2.8)
\]
記号
| xα0 | : 前述による。 |
| N0 | : 柱軸力 |
| Lx | : x方向の基礎幅 |
| ax | : x方向の柱幅 |
| xxn | : x方向圧縮縁から中立軸までの距離 |
|
i) xe0/Lx ≦ 1/6の時
\[
_{x}x_{n} = \frac{L_{x}}{2}(1+\frac{L_{x}}{6_{x}e_{0}}) ・・・・(2.9)
\]
ii) xe0/Lx > 1/6の時
\[
_{x}x_{n} = 3(\frac{L_{x}}{2} - _{x}e_{0}) ・・・・(2.10)
\]
※偏心が生じない(xe0=0)の時はxn=∞となり、地反力の分布は等分布になります。
※xe0/Lx > 0.3となる場合は計算不可
|
(3) 基礎設計用のせん断応力の計算は式(2.11)によります。
(X方向の最大せん断応力の計算)
\[
_{x}Q_{F} = N_{0}\frac{(1+_{x}α_{0})}{2}(1 - \frac{1}{4}\frac{L_{x}-a_{x}}{_{x}x_{n}})\frac{L_{x}-a_{x}}{L_{x}}・・・・(2.11)
\]
記号
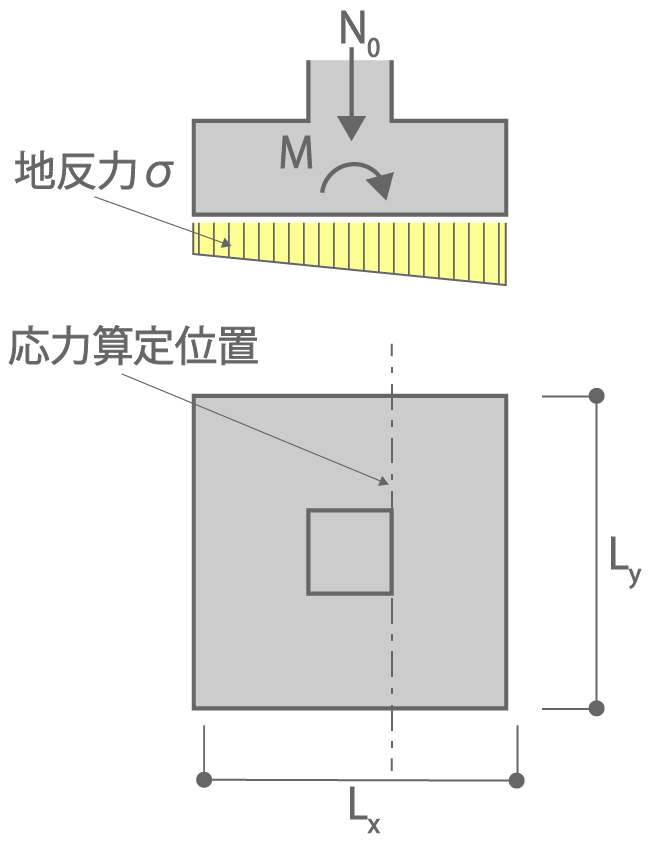
図2.2 基礎スラブの応力算定位置
2.2 曲げの検討
鉄筋の許容引張応力度が曲げ引張応力度は以下であることを確認します。曲げ引張応力度は(2.9)式によります。
(X方向の最大せん断応力の計算)
\[
σ_{t} = \frac{M_{F}}{ja_{t}}・・・・(2.12)
\]
記号
| MF | : 前述による。 |
| j | : 応力中心間距離(=(7/8)d) |
| d | : 基礎スラブの有効せい(=D1>+D1-dt) |
| dt | : 基礎スラブ下端からベース筋重心位置までの距離 |
| at | : 引張鉄筋の全断面積 |
2.3 せん断の検討
基礎スラブの許容せん断力が、せん断応力QF未満であることを確認します。許容せん断力Qaは式(2.10)によります。
\[
Q_{a} = Lf_{s}j・・・・(2.13)
\]
記号
| Qa | : 基礎スラブの許容せん断力 |
| L | : 基礎スラブの幅 |
| fs | : コンクリートの許容せん断応力度 |
| j | : 前述による |
2.4 付着の検討
基礎スラブの付着の検討は、最大付着応力度の検討(RC規2018 (16.1),(16.3))と平均付着応力度の検討(RC規2018 (16.2),(16.4))を行います。いづれかがOKであれば、タブはOKアイコンになります。
(1) 最大付着応力度に対する検討
\[
τ_{a1} = \frac{Q_{F}}{ΣΨ・j} ≦ f_{a}・・・・(2.14)
\]
記号
| QF | : 基礎の設計用せん断力 |
| ΣΨ | :全引張鉄筋の周長の合計 |
| j | : 前述による。 |
(2) 平均付着応力度に対する検討
\[
τ_{a2} = \frac{σ_{t}・d_{b}}{4(l_{d}-d)} ≦ 0.8f_{a}・・・・(2.15)
\]
記号
| σt | : ベース筋の引張応力度式(2.12)による。「鉄筋末端にフックを設ける」にチェックを入れた場合は式(2.12)より求めた引張応力度を2/3に低減する。 |
| db | : 鉄筋の呼び径 |
| ld | : ベース筋の付着長さ〔図2.2〕参照 |
|  図2.3 基礎スラブの応力算定位置 |
| d | : 基礎スラブの有効せい。入力指定により、0にすることも可能 |
| fa | : 鉄筋の許容付着応力度 |
2.5 パンチングの検討
基礎スラブのパンチングの検討は式(2.16)を確認します。
\[
N_{0} ≦ Q_{pa} = 1.5b_{0}jf_{s}・・・・(2.16)
\]
記号
| N0 | : 柱軸力 |
| Opa | : 基礎スラブのパンチングシアに対する許容せん断力 |
| b0 | : パンチングシアに対する設計用せん断力算定面の延べ幅〔図2.3〕参照 |
|  図2.4 基礎スラブの応力算定位置 |
| その他は前述による |
STRUCTURAL DESIGN APPS
