胴縁の設計

データ名：---

プロジェクト名：---

更新日：---

Proにアップグレードすれば全ての機能が使えます!

新しいデータ

名称

Alert

基本事項

接続条件
l(m)

胴縁ピッチ

横座屈を考慮する。

lb(m)

断面種別
断面

D(mm)
t(㎜)
r(mm)

端部ボルト本数
端部ボルト径

ボルト種別
接合条件

荷重入力

壁自重(N/㎡)
風圧力(N/㎡)

クライテリア

・長期

長期許容変形角
長期許容たわみ

・短期

短期許容変形角
短期許容たわみ

断面性能/荷重

f_t(長期) =N/㎟

f_t(短期) =N/㎟

f_b(長期) =N/㎟

f_b(短期) =N/㎟

qa(短期) =kN/本

I_x =cm⁴

I_y =cm⁴

Z_x =cm³

Z_y =cm³

A =cm²

i_y =cm

J =cm⁴

λ_y =

W_自重 =N/m

長期(弱軸方向)荷重 =kN/m

短期(強軸方)荷重 =kN/m

曲げ

・常時 :

M_弱軸 = kNm

σ_b弱軸 = N/㎟

→σ_b弱軸/f_t =

・風荷重時 :

M_強軸 = kNm

σ_b強軸 = N/㎟

→σ_b強軸/f_b + σ_b弱軸/f_t =

せん断

・風荷重時 :

Q_強軸 = kN → Q_強軸/Q_a =

たわみ

・常時 :

δ_弱軸 =㎜ ( δ_弱軸/l = )

・風荷重時 :

δ_強軸 =㎜

→ δ(= √(δ_弱軸²+δ_強軸²) ) =㎜

( δ/l = )

解説

入力内容の解説
計算内容の解説
規基準
参考文献

梁種別	: 単純梁と2連梁から選択します
l	: 下図によります。

胴縁ピッチ	: 胴縁の間隔を指定します。
lb	: 座屈長さ(m)、0にすると横座屈を考慮しません。
断面種別	: リップ溝形鋼,角形鋼管から選択できます。
断面	: 各種断面寸法の入力値は下記によります。

	角形鋼管
端部ボルト	: 本数、径、種別、接合条件(1面せん断 or 2面せん断)を指定します。

許容曲げ応力度f_bの計算

a)リップ溝型鋼

鋼構造許容応力度設計規準の方法によります。本アプリでは_pλ_b=0.3、C=1.0で計算しています。

λ_b≧_pλ_bのとき

\[ f_{b} = \frac{F}{ν} \]

_pλ_b<λ_b≦_eλ_bのとき

\[ f_{b} = \frac{\left\{1 - 0.4\frac{λ_{b}ー_{p}λ_{b}}{_{e}λ_{b} - _{p}λ_{b}}\right\}F}{ν} \]

_eλ_b<λ_bのとき

\[ f_{b} = \frac{1}{λ^{2}_{b}}・\frac{F}{2.17} \]

ここに

\[ λ_{b} = \sqrt{\frac{M_{y}}{M_{e}}} \] \[ M_{e} = C\sqrt{\frac{π^{4}EI_{Y}・EI_{w}}{l_{b}^{4}}+\frac{π^{2}EI_{Y}・GJ}{l^{2}_{b}}} \] \[ _{p}λ_{b} = \frac{1}{\sqrt{0.6}} \]

i) 補剛区間内で曲げモーメントが単調に変化する場合

\[ _{p}λ_{b} = 0.6 + (\frac{M_{2}}{M_{1}}) \] \[ C = 1.75 + 1.05(\frac{M_{2}}{M_{1}}) + 0.3(\frac{M_{2}}{M_{1}})^{2} ≦ 2.3 \]

ii) 補剛区間内で曲げモーメントが単調に変化する場合

\[ _{p}λ_{b} = 0.3 \] \[ C = 1.0 \]

記号

f_b	: 許容曲げ応力度
λ_b	: Myに対する曲げ材の基準化細長比
l_b	: 圧縮フランジの支点間距離
ν	: 安全率(ν = 3/2 + (2/3)(λ_b/_eλ_b)²)
_eλ_b	: 弾性限界細長比
_pλ_b	: 塑性限界細長比
M_e	: 弾性横座屈モーメント
M_y	: 降伏モーメント(M_y=F・Z)
Z	: 断面係数
C	: 弾性横座屈モーメントの補正係数
I_Y	: 弱軸まわりの断面二次モーメント
I_w	: 曲げねじり定数
G	: せん断弾性係数
J	: サンブナンのねじり定数
M1、M2	: それぞれ座屈補剛区間の両端に作用する大きいほう、小さいほうの、橋軸まわりの曲げモーメント。 M2/M1は複曲率の場合は正、単曲率の場合は負となる。

b)角形鋼管

許容曲げ応力度fbはftとします。

ボルト・高力ボルトの許容応力

高力ボルト及び、普通ボルトの許容せん断耐力は下記によります。

高力ボルトの許容せん断耐力
高力ボルトの鋼種	ボルト呼び径	許容せん断力(kN/本)
		長期			短期
		許容せん断力		許容引張力
		1面摩擦	2面摩擦	許容引張力
F8T(溶融亜鉛めっきボルト)	M12	12.1	24.1	28.2	長期の1.5倍
	M16	21.4	42.9	50.3
	M20	33.5	67.0	78.5
	M22	40.5	81.1	95.0
	M24	48.2	96.4	113
	M27	61.0	122.0	143
	M30	75.4	151.0	177
F10T	M12	17.0	33.9	35.1
	M16	30.2	60.3	62.3
	M20	47.1	94.2	97.4
	M22	57.0	114.0	118
	M24	67.9	136.0	140
	M27	85.9	172.0	177
	M30	106.0	212.0	219

普通ボルトの許容せん断耐力
強度区分	ボルト呼び径	許容耐力(kN/本)
		長期			短期
		せん断力		許容引張力
		1面せん断	2面せん断	許容引張力
4.6、4.8	M12	7.79	15.6	13.5	長期の1.5倍
	M16	14.5	29.0	25.1
	M20	22.6	45.3	39.2
	M22	28.0	56.0	48.5
	M24	32.6	65.2	56.5
	M27	42.4	84.8	73.4
	M30	51.8	104	89.8
5.6、5.8	M12	9.73	19.5	16.9
	M16	18、1	36.3	31.4
	M20	28.3	56.6	49.0
	M22	35.0	70.0	60.6
	M24	40.8	81.5	70.6
	M27	53.0	106.0	91.8
	M30	64.8	130.0	112
6.8	M12	13.6	27.3	23.6
	M16	25.4	50.8	44.0
	M20	39.6	79.2	68.6
	M22	49.0	98.0	84.8
	M24	57.1	114.0	98.9
	M27	74.2	148.0	129
	M30	90.7	181.0	157

曲げ応力度の計算

胴縁の曲げ応力度は下記によります。

a)常時(長期)

σ_bL = M_弱軸/z_y

ここで、

σ_bL	: 長期最大曲げ応力度
Z_y	: 弱軸の断面係数
M_y	: 弱軸方向最大曲げ応力で下記によります
	M_y = Wy*l²/8
l	: 部材長
wy	: 固定荷重(N/m)(図1)

b)風荷重時(短期)

σ_bS = M_強軸/z_x + M_弱軸/z_y

ここで、

σ_bS	: 短期の最大曲げ応力度
Z_x	: 強軸の断面係数
M_x	: 強軸方向最大曲げ応力で下記によります
	M_x = W*l²/8
wx	: 風荷重(N/m)(図1)
その他は前出によります。

せん断力の計算

胴縁の最大せん断力は下記によります。

a)単純梁

Q_強軸 = w_x*l/2

b)2連梁

Q_強軸 = 5*w_x*l/4

ここで、

Q_強軸	: x方向最大せん断力
w_x	: 風荷重(N/m)(図1)
l	: 部材長

たわみの計算

胴縁の最大たわみは下記により計算します。

a)常時(長期)

a-i)単純梁

δ_弱軸 = w_x*l⁴/(384*E*I_y)

a-ii)2連梁

δ_弱軸 = w_y*l⁴/(185*E*I_y)

ここで、

δ_弱軸	: 弱軸方向最大たわみ
w_y	: 固定荷重
l	: 部材長
E	: ヤング係数
I_y	: 弱軸方向の断面二次モーメント

b)風荷重時(短期)

δ_max = √(δ_弱軸² + δ_強軸²)

ここで、

δ_max	: 組み合わせによる最大たわみ
δ_強軸	: 強軸方向最大たわみで以下によります
	b-i)単純梁 δ_強軸 = w_xl⁴/(384EI_x) b-ii)2連梁 δ_強軸 = w_xl⁴/(185EI_x)
w_x	: 風荷重(N/m)(図1)
I_x	: 強軸方向の断面二次モーメント
その他は前出によります。

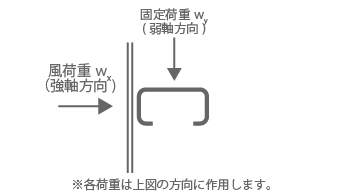
図1 胴縁荷重図

告示平12建告第1459号

建築物の使用上の支障が起こらないことを確かめる必要がある場合及びその確認方法を定める件

建築基準法施行令（昭和二十五年政令第三百三十八号）第82条第四号の規定に基づき、建築物の使用上の支障が起こらないことを確かめる必要がある場合及びその確認方法を次のように定める。

第1 建築基準法施行令（以下「令」という。）第82条第四号に規定する使用上の支障が起こらないことを検証することが必要な場合は、建築物の部分に応じて次の表に掲げる条件式を満たす場合以外の場合とする。

建築物の部分

条件式

木造

はり(床面に用いるものに限る。以下この表において同じ。)

D/l>1/12

鉄骨造

デッキプレート版(床版としたもののうち平成14年国土交通省告示第326号の規定に適合するものに限る。以下同じ

t/lx>1/25

はり

D/l>1/12

鉄筋コンクリート造

床版(片持ち以外の場合)

t/lx>1/30

床版(片持ちの場合)

t/lx>1/10

はり

D/l>1/10

鉄骨鉄筋コンクリート造

はり

D/l>1/12

アルミニウム合金造

はり

D/l>1/10

軽量気泡コンクリートパネルを用いた構造

床版

t/lx>1/25

この表において、t、lx、D及びlは、それぞれ以下の数値を表すものとする。

t	床版の厚さ(単位ミリメートル)
lx	床版の短辺方向の有効長さ(デッキプレート床版又は軽量気泡コンクリートパネルにあっては、支点間距離)(単位ミリメートル)
D	はりのせい(単位ミリメートル)
l	はりの有効長さ(単位ミリメートル)

第2 令第82条第四号に規定する建築物の使用上の支障が起こらないことを確認する方法は、次のとおりとする。

一当該建築物の実況に応じた固定荷重及び積載荷重によってはり又は床版に生ずるたわみの最大値を計算すること。ただし、令第85条の表に掲げる室の床の積載荷重については、同表（は）欄に定める数値によって計算することができる。

二前号で求めたたわみの最大値に、構造の形式に応じて次の表に掲げる長期間の荷重により変形が増大することの調整係数（以下「変形増大係数」という。）を乗じ、更に当該部材の有効長さで除して得た値が250分の1以下であることを確認すること。ただし、変形増大係数を載荷実験により求めた場合においては、当該数値を用いることができる。

構造の形式		変形増大係数
木造		2
鉄骨造		1(デッキプレート版にあっては1.5)
鉄筋コンクリート造	床版	16
	はり	8
鉄骨鉄筋コンクリート造		4
アルミニウム合金造		1
軽量気泡コンクリートパネルを用いた構造		1.6

1) (社)日本建築学会、鋼構造許容応力度設計基準、2019.10

2) 全国官報販売協同組合、2020年版建築物構造関係技術基準解説書、2022.11

名称

Alert

基本事項

接続条件
l(m)

胴縁ピッチ

横座屈を考慮する。

lb(m)

断面種別
断面

D(mm)
t(㎜)
r(mm)

端部ボルト本数
端部ボルト径

ボルト種別
接合条件

荷重入力

壁自重(N/㎡)
風圧力(N/㎡)

クライテリア

・長期

長期許容変形角
長期許容たわみ

・短期

短期許容変形角
短期許容たわみ

断面性能/荷重

f_t(長期) =N/㎟

f_t(短期) =N/㎟

f_b(長期) =N/㎟

f_b(短期) =N/㎟

qa(短期) =kN/本

I_x =cm⁴

I_y =cm⁴

Z_x =cm³

Z_y =cm³

A =cm²

i_y =cm

J =cm⁴

λ_y =

W_自重 =N/m

長期(弱軸方向)荷重 =kN/m

短期(強軸方)荷重 =kN/m

曲げ

・常時 :

M_弱軸 = kNm

σ_b弱軸 = N/㎟

→σ_b弱軸/f_t =

・風荷重時 :

M_強軸 = kNm

σ_b強軸 = N/㎟

→σ_b強軸/f_b + σ_b弱軸/f_t =

せん断

・風荷重時 :

Q_強軸 = kN → Q_強軸/Q_a =

たわみ

・常時 :

δ_弱軸 =㎜ ( δ_弱軸/l = )

・風荷重時 :

δ_強軸 =㎜

→ δ(= √(δ_弱軸²+δ_強軸²) ) =㎜

( δ/l = )

胴縁の設計

コピー元のデータを選択してください。

削除するデータを選択してください。

Alert

基本事項

荷重入力

クライテリア

断面性能/荷重

曲げ

せん断

たわみ

許容曲げ応力度fbの計算

ボルト・高力ボルトの許容応力

曲げ応力度の計算

せん断力の計算

たわみの計算

Alert

基本事項

荷重入力

クライテリア

断面性能/荷重

曲げ

せん断

たわみ

許容曲げ応力度f_bの計算