STRUCTURAL DESIGN APPS

Guest

Guest User
Login
SignUp

片持ち擁壁の設計

データ名：---
プロジェクト名：---
更新日：---
Proにアップグレードすれば全ての機能が使えます!
コピー元のデータを選択してください。
削除するデータを選択してください。

入力

躯体形状

  • Hf(㎜)
  • L2(㎜)
  • T2(㎜)
  • T3(㎜)
  • D2(㎜)

擁壁断面図

背面土の状態

断面算定条件

  • γC(kN/㎡)
  • ピッチ
  • ピッチ
  • 材種
  • 材種

安全率

・常時

土圧の計算(安定計算,底盤設計用,土と土)

・ 常時

δL = ° KAL =

PAL =

kN

PALH =

kN


PALV =

kN

PqLH =

kN

土圧の計算(たて壁計算用,土とコンクリート)

α = °

・ 常時

δL = ° KAL =

PAL =

h2kN

PALH =

h2kN


PALV =

h2kN

PqLH =

hkN

自重の計算

区分断面積
W(㎡)		単位重量
γ(kN/㎡)		鉛直力
V(kN)		水平力
H=V・kh(kN)		原点からの
合力作用位置(m)		原点に対する
回転モーメントの距離
(kNm)
XYVxVy
W1
W2
W3
W4
W5
W6
合計
原点からの
重心位置

XG = totalVx/totalV = m

YG = totalVy/totalV = m

・常時

荷重鉛直力
V(kN)		水平力
H(kN)		原点からの
合力作用位置(m)		原点に対する
回転モーメント
(kNm)
滑動・転倒
検討用		支持力
検討用		XY抵抗モーメント
Mr		転倒モーメント
M0
自重---
載荷重0.00---
土圧
載荷重土圧---
合計
安定
計算		 転倒 d = (Mr-M0)/V = ㎜ e = LW/2-d = LW/6 =
Mr/M0 =
滑動 FS = ΣV・μ/ΣH =
支持力 q1,q2 = kN/㎡,kN/㎡ kN/㎡

たて壁の設計

at = ㎟/m

・常時

ft = N/㎟fs = N/㎟

MhL = PALH・h/3 + PqLH ・ h/2 = h3/3 + h2/2

QhL = PALH + PqLH = h2 + h

(i)壁中間(h = m, j = ㎜)

MhL = kNm

MAL = kNm

MhL/MAL =

QhL = kN

QAL = kN

QhL/QAL =

(ii)壁端部(h = m, j = ㎜)

MhL = kNm

MAL = kNm

MhL/MAL =

QhL = kN

QAL = kN

QhL/QAL =

底盤の設計

at = ㎟/mj = ㎜

・自重による底盤の曲げ応力

(i)A-A断面

区分面積
W(㎡)		単位重量
γ(kN)		QwアームxMw
長期短期長期短期
W2
W6
合計

(ii)B-B断面

区分面積
W(㎡)		単位重量
γ(kN)		QwアームxMw
長期短期長期短期
W4
W5
載荷重--
土圧--
合計

・常時

ft = N/㎟fs = N/㎟

(i)A-A断面

qA = kN/㎡

Mq = kNm

ML = Mq - MW = kNm

MAL = kNm

ML/MAL =

Qq = kN

QL = Qq - QW = kN

QAL = kN

QL/QAL =

(ii)B-B断面

qB = kN/㎡

Mq = kNm

ML = Mq - MW = kNm

MAL = kNm

ML/MAL =

Qq = kN

QL = Qq - QW = kN

QAL = kN

QL/QAL =


解説 トップに戻る
  • 記号の解説
  • 計算内容の解説
  • 規基準
  • 参考文献
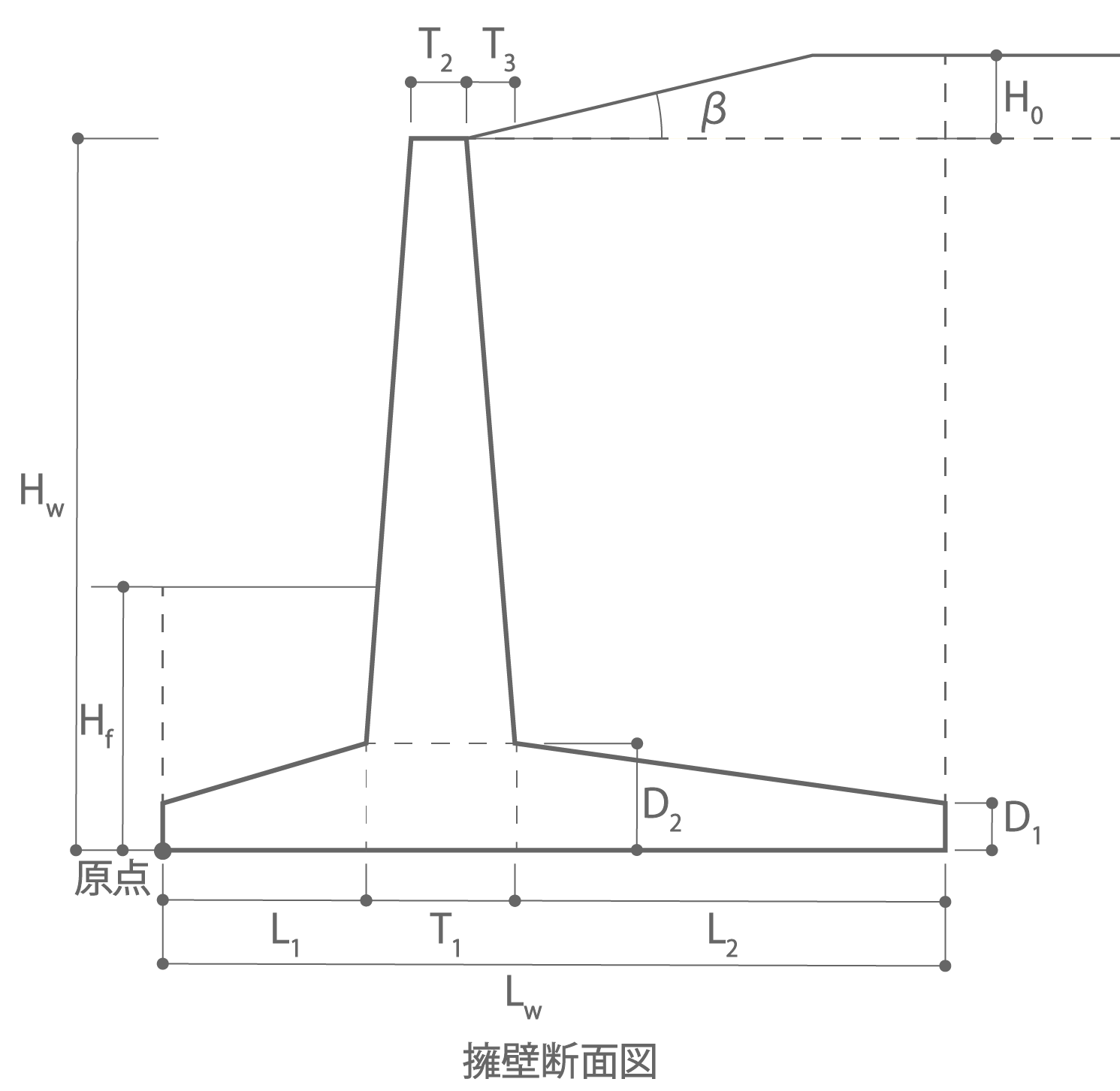
HW:擁壁全髙
Hf:根入れ深さ
L1:底盤左側長さ
L2:底盤右側長さ
T1:たて壁元端厚さ
T2:たて壁先端厚さ
T3:たて壁先端と元端のずれ寸法
D1:底盤先端の厚さ
D2:底盤元端の厚さ
FC:コンクリートの設計基準強度
γC:コンクリートの単位体積重量
β:背面土の法面傾斜角
H0:背面土の余盛高さ
KA:土圧係数
φ:内部摩擦角
γs:土の単位体積重量
Kh:水平震度
μ:基礎底面と地盤の摩擦係数
lfe:地盤の長期許容地耐力
α:壁背面と鉛直面のなす角
δ:壁面摩擦角
ω:背面土の滑り角
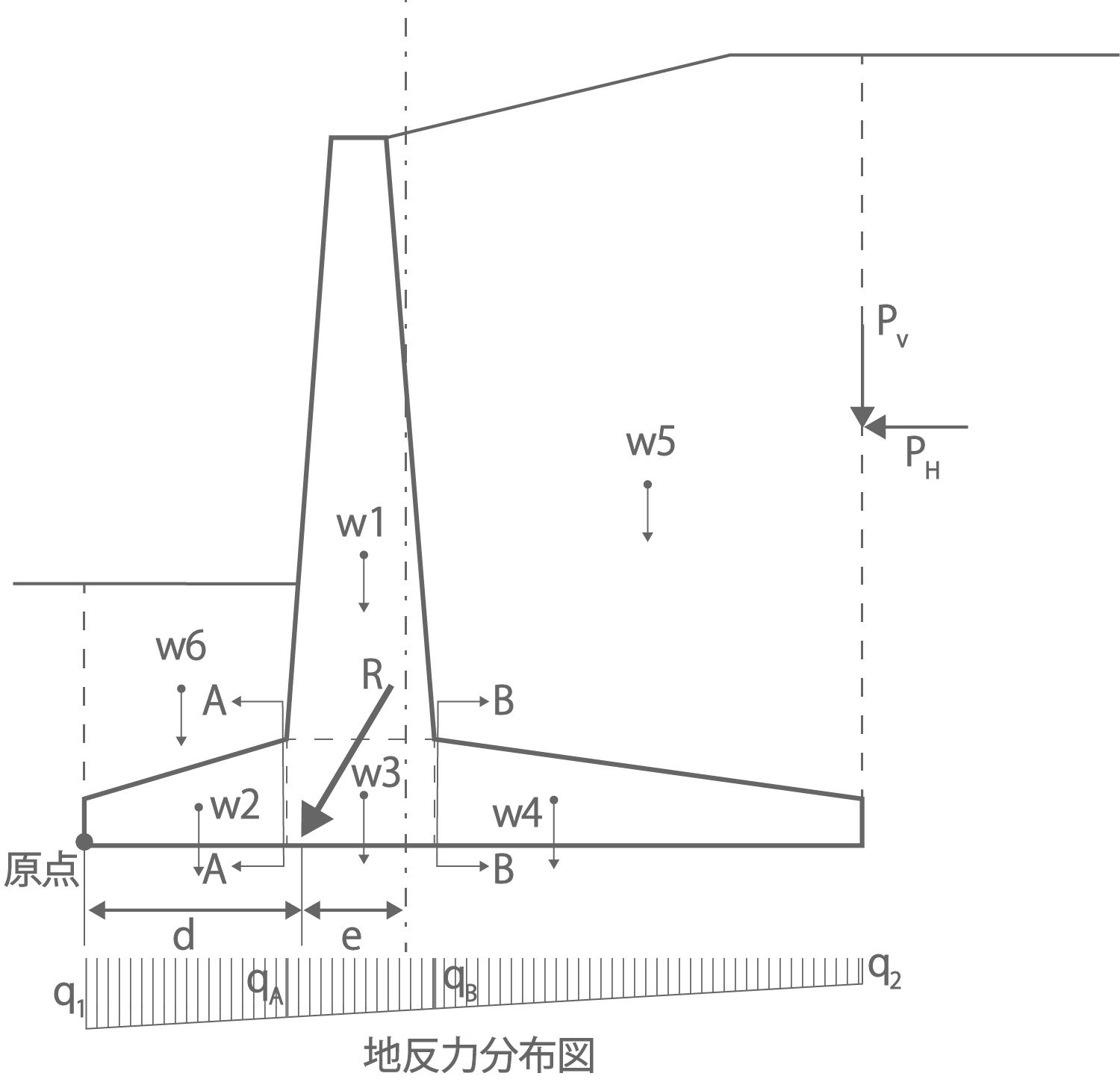
W1～W6:擁壁・埋め戻し土の自重
q:地表面載荷重
PA:主働土圧による合力
PqH:地表面載荷重による合力の水平成分
Pv:土圧合力の鉛直成分
PH:土圧合力の水平成分
tPH:擁壁天端に作用する水平力
R:全荷重合力
d:原点から荷重合力作用位置までの距離
e:全荷重合力の作用位置と、擁壁重心位置の距離
Mr:原点まわりの抵抗モーメント
M0:原点まわりの転倒モーメント
V:鉛直荷重の合力
H:水平力の合力
Fs:滑動に対する安全率
q1,q2:擁壁底盤端部における地盤反力
Mh:たて壁の設計用曲げモーメント
Qh:たて壁の設計用せん断力
h:たて壁天端から検討位置までの距離
MW:土、擁壁自重による底盤の曲げ応力
Mq:地反力による底盤の曲げ応力
MA:部材の許容曲げモーメント(=at・ft・j)
QA:部材の許容せん断力(=fs・j)
at:単位幅あたりの引張鉄筋の断面積の合計
ft:鉄筋の許容引張力
dt:躯体の引張縁から鉄筋の重心位置までの距離
j:鉄筋の応力中心間距離
fs:コンクリートの許容せん断力

目次

1. 主働土圧の計算方法

主働土圧の計算方法は「クーロン式」、「試行くさび法」、「直接入力」から選択します。

1.1. クーロン式

a. 常時

クーロン式による土圧は以下により計算します。

\[ \begin{aligned} 主働土圧 : P_{A} = \frac{1}{2}γ_{S}・K_{A}・H^2 ・・・・(1.1.1)\\ 載荷重による土圧 : P_{qH} = q・K_{A}・H ・・・・(1.1.2) \end{aligned} \]

記号

γS : 背面土の単位体積重量
KA : 常時主働土圧係数、式(1.2.3)によります。
\[ K_{A} = \frac{cos^2(φ-α)}{cos^2α・cos(α+δ)\left[1+\sqrt{\frac{sin(φ+δ)・sin(φ-β)}{cos(α+δ)・cos(α-β)}}\right]^2} ・・・・(1.1.3) \]

記号

φ : 背面土の内部摩擦角
α : たて壁の鉛直面とのなす角
β : 背面土の法面と水平面とのなす角
δ : 壁面摩擦角〔図１.1〕
q : 地表面載荷重
H :土圧の計算に用いる擁壁の高さ

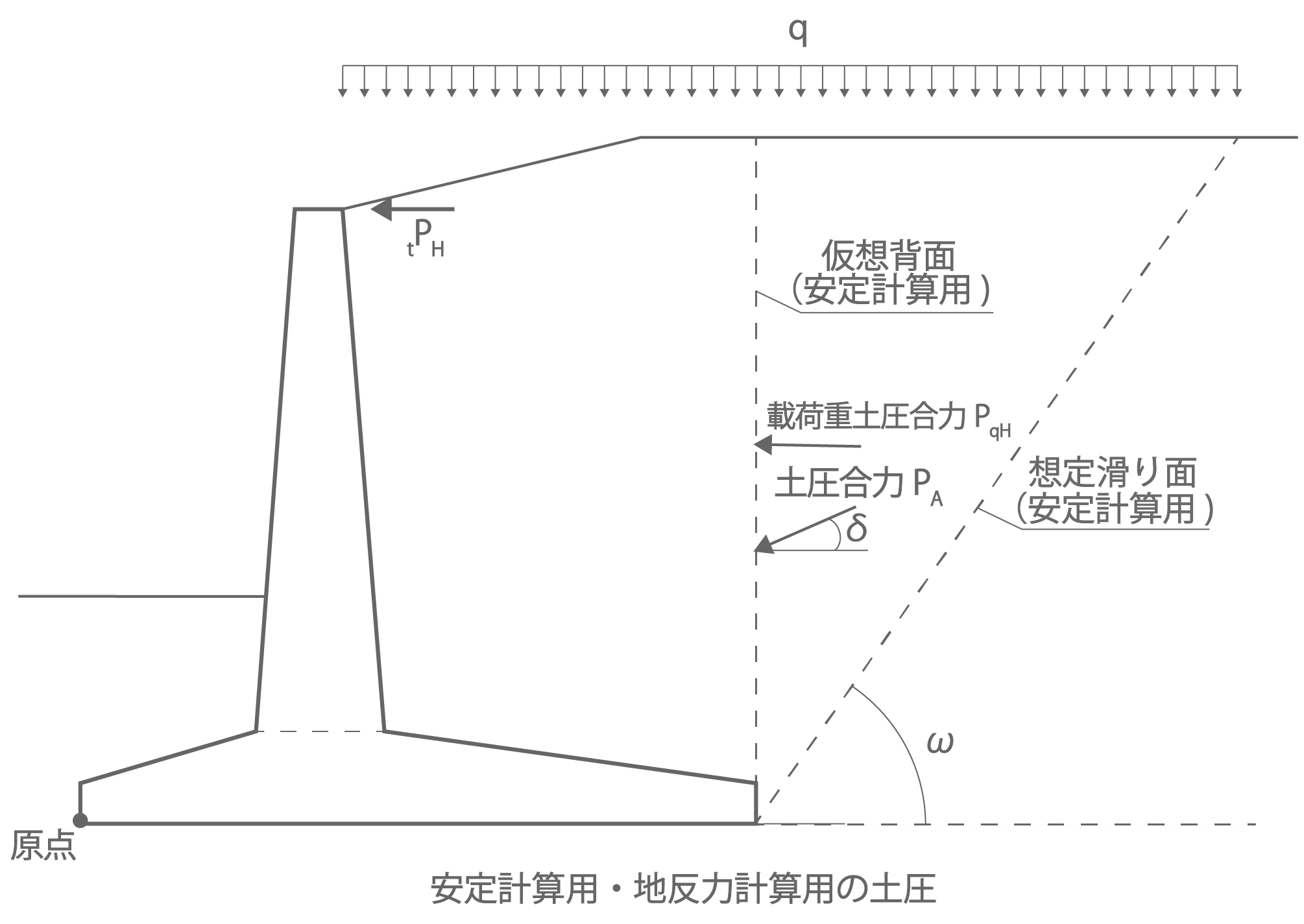
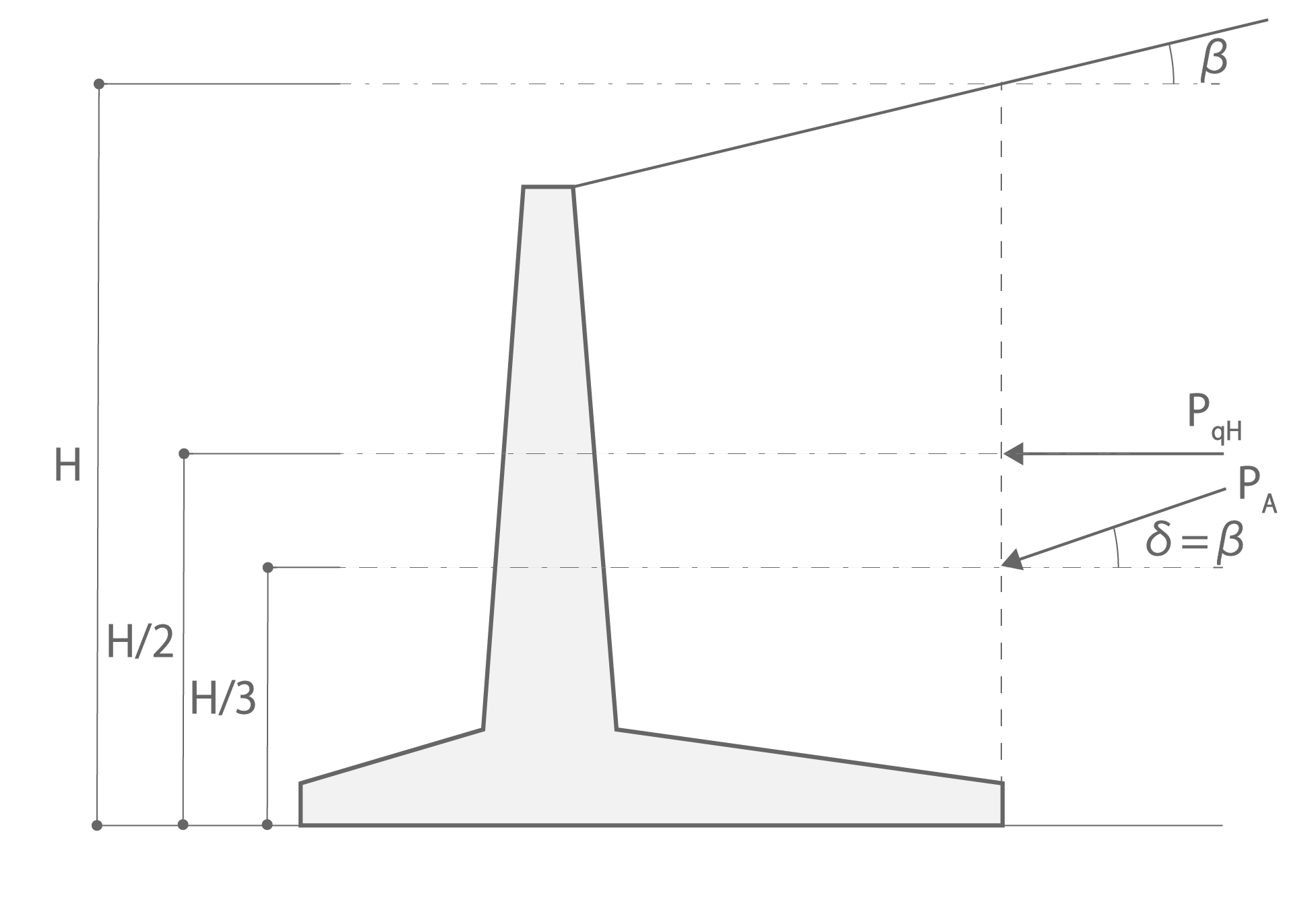(a) 安定計算用の土圧合力

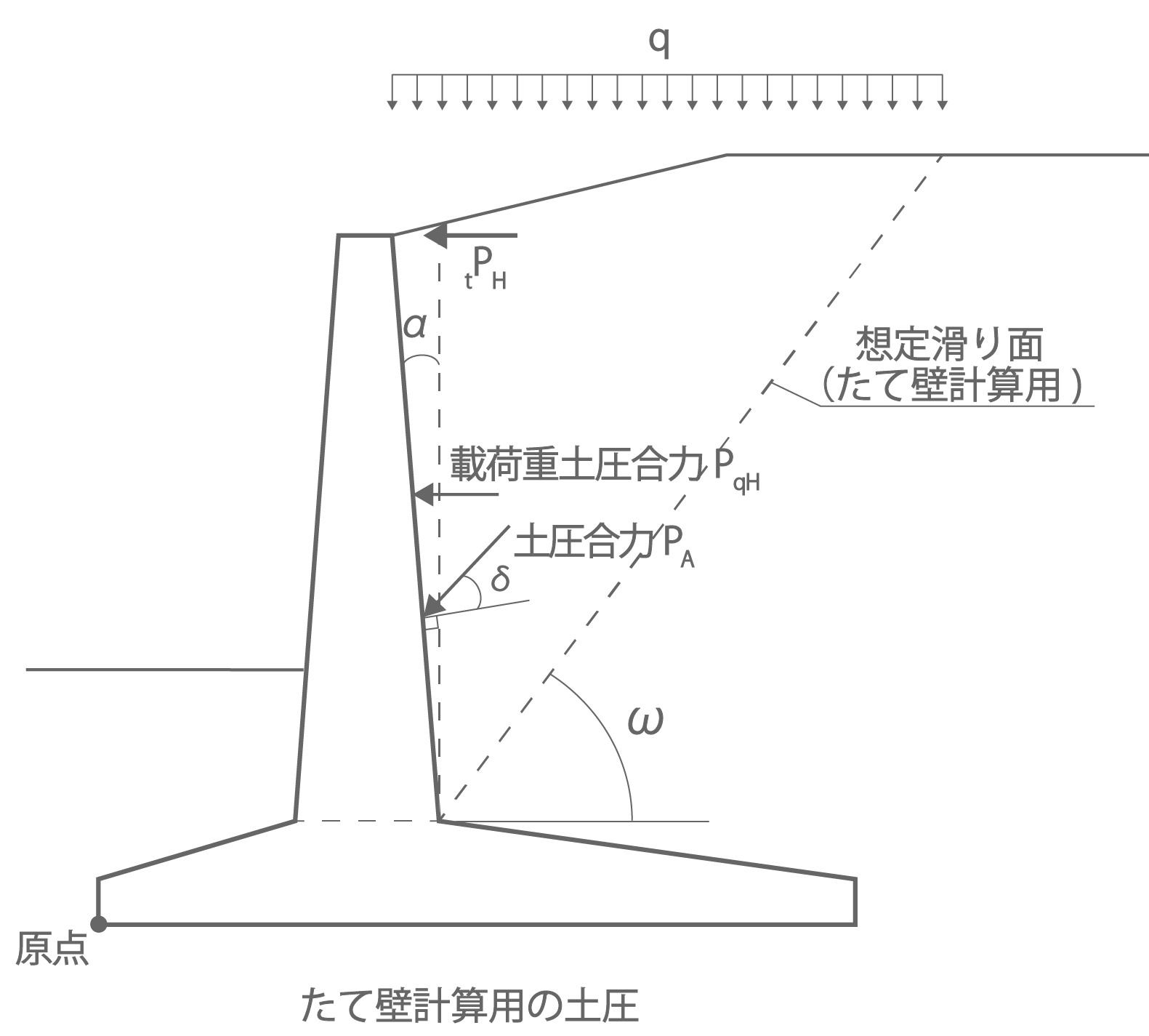
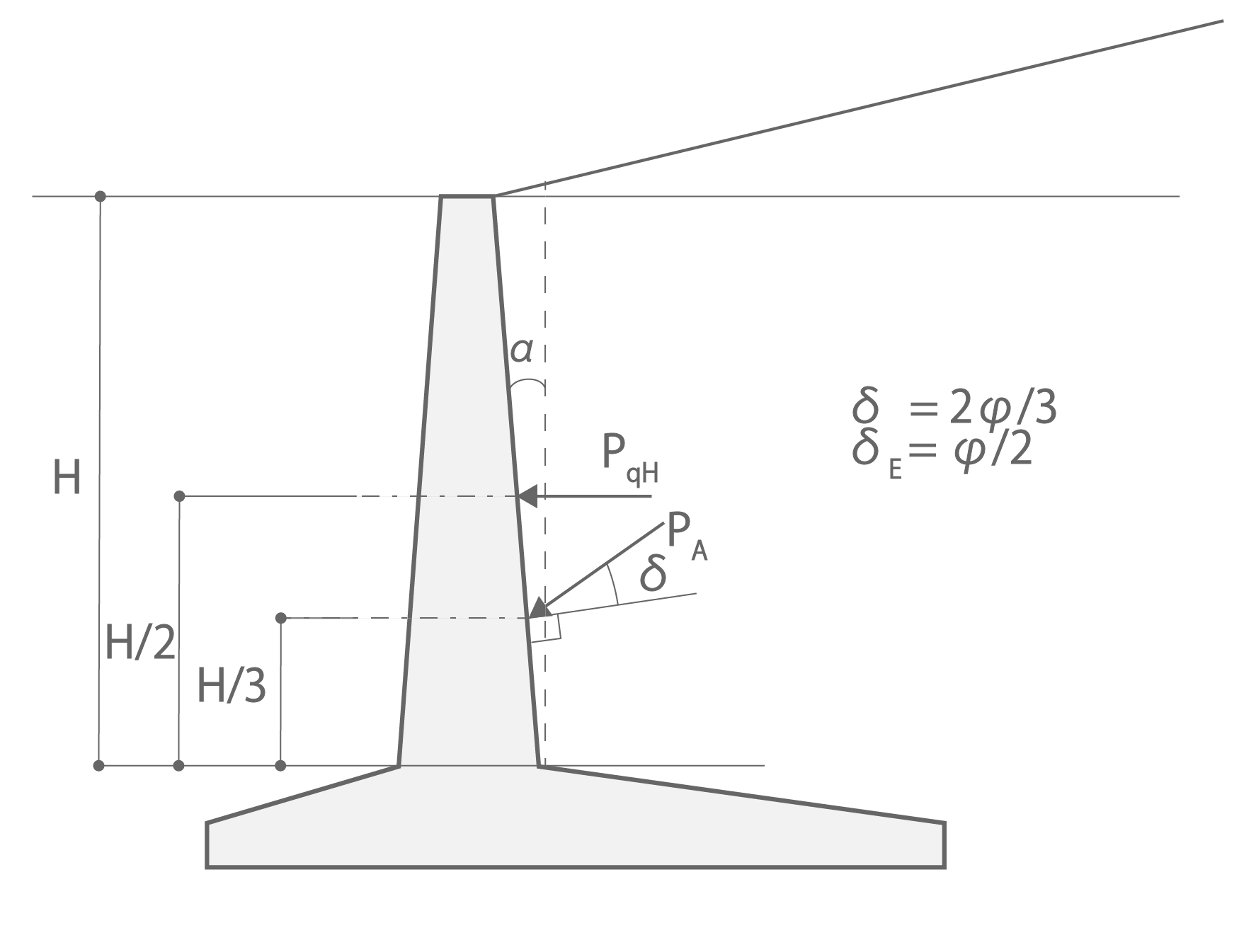(b) たて壁設計用土圧合力

図1.1 クーロン土圧

※クーロン式では φ>β である必要があります。

b. 地震時(物部・岡部式）

クーロン式による土圧を選択した場合、地震時の土圧は物部・岡部式を採用します。

\[ \begin{aligned} 主働土圧 : P_{AE} = \frac{1}{2}γ_{S}・K_{AE}・H^2 ・・・・(1.1.4)\\ 載荷重による土圧 : P_{qHE} = q_{E}・K_{AE}・H ・・・・(1.1.5) \end{aligned} \]

記号

KAE : 地震時主働土圧係数、式(1.1.6)によります。
\[ K_{AE} = \frac{cos^2(φ-α―Θ)}{cosΘ・cos^2α・cos(α+δ_{E}＋Θ)\left[1+\sqrt{\frac{sin(φ+δ_{E})・sin(φ-βーΘ)}{cos(α+δ_{E}＋Θ)・cos(α-β)}}\right]^2}・・・・(1.1.7) \]

記号

Θ : 地震合成角（=tan-1kh）
kh : 設計水平震度
δE : 地震時壁面摩擦角

・安定計算用

\[ δ_{E} = tan^-1\left(\frac{sinφ・sin(Θ + Δ-β)}{1-sinφ・cos(Θ+Δ-β)}\right)・・・・(1.1.8) \]

ここに

\[ Δ = sin^-1\left(\frac{sin(β+Θ)}{sinφ}\right)・・・・(1.1.9) \]

・たて壁設計用

\[ δ_{E} = \frac{φ}{2}・・・・(1.1.10) \]
その他の記号は前出によります。

※物部・岡部式では90°>α+δE+Θかつφ≧β+Θの条件を満たす必要があります。

1.2. 試行くさび法

1.2.1 土圧合力の計算方法

a) 常時

試行くさび法は、力の三角形〔図1.2〕から主働土圧が最大となるωを求める計算方法です。主働土圧の計算は式(1.2.1),土圧係数は(1.2.2)によります。なお載荷重による土圧は式(1.1.2)によります。

\[ \begin{aligned} P_{A}sin(90°-(ω-φ)+δ+α) = Wsin(ω-φ)\\ \therefore P_{A} = \frac{Wsin(ω-φ)}{cos(ω-φ-δ-α)}・・・・(1.2.1)\\ K_{A} = \frac{2P_{A}}{γH^2}・・・・(1.2.2) \end{aligned} \]

記号

PA : 主働土圧合力
ω : 想定滑り面と水平面のなす角
φ : 内部摩擦角
δ : 壁面摩擦角（安定計算用:「1.2.2 土くさびの重量Wと常時のδの計算」によります,たて壁設計用:2φ/3）
α : 鉛直面と壁面とのなす角
W : 土くさびの重量（1.2.2 土くさびの重量Wと常時のδの計算 によります）

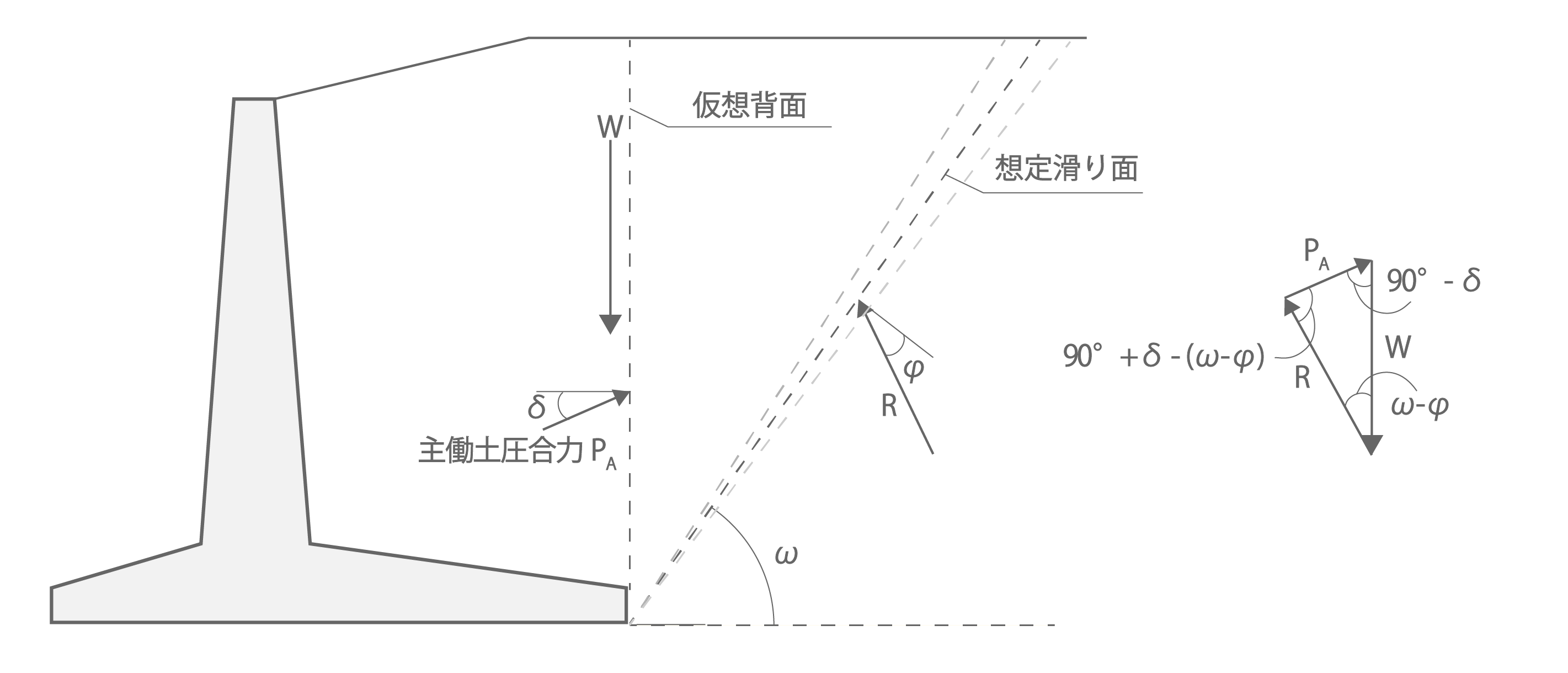(a) 安定計算用

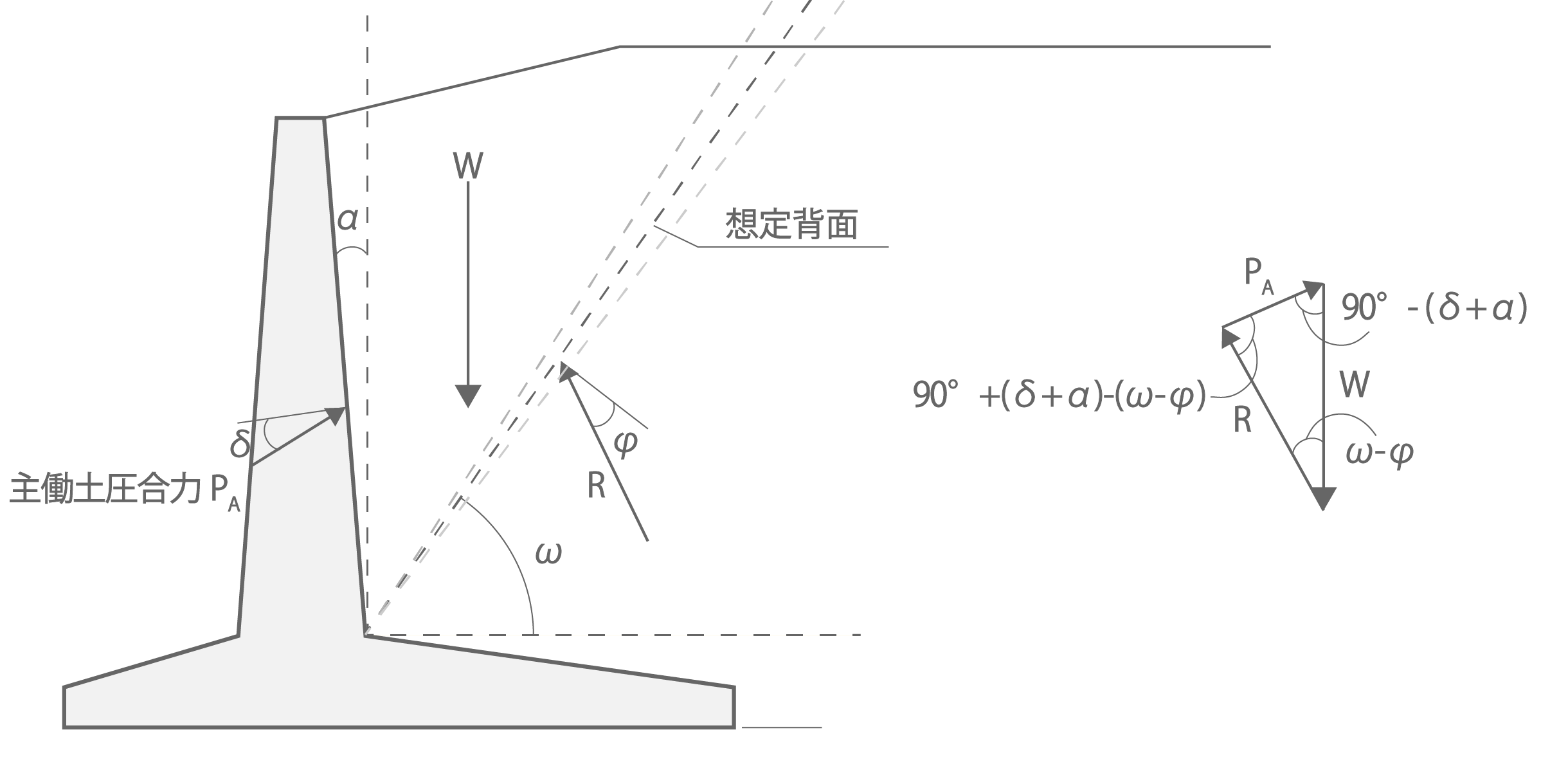(b) たて壁設計用

図1.2 試行くさび法による力の三角形
b) 地震時

地震時の土圧合力は地震時の慣性力を考慮した力の三角形〔図1.2〕から主働土圧が最大となるωを求めます。なお載荷重による土圧は式(1.1.5)によります。

\[ P_{AE} = \frac{Wsin(ω+Θ-φ)}{cos(Θ)・cos(ω-φ-δ_{E}-α)}・・・・(1.2.3) \] \[ K_{AE} = \frac{2P_{AE}}{γH^2}・・・・(1.2.4) \]

記号は前出による

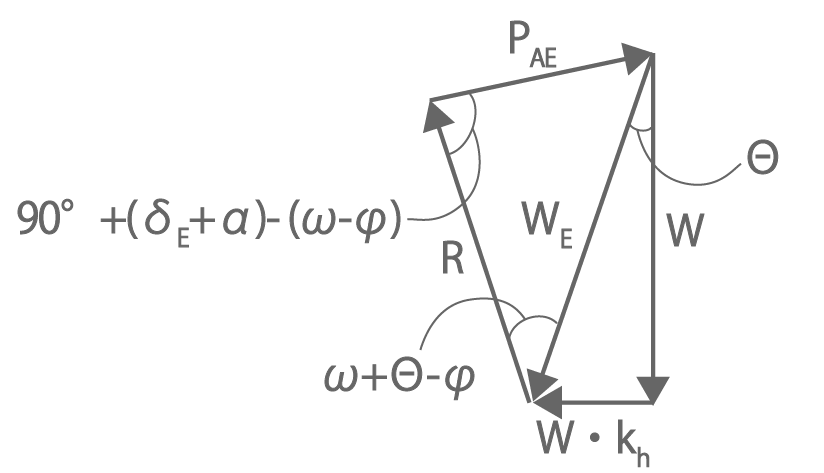
図1.3 地震時の力の三角形

1.2.2 土くさびの重量Wと常時のδの計算

a) 安定計算用

安定計算用の土くさびの重量および常時のδは背面土の状態および想定すべり角の大きさによりケース1～4のいづれかにより計算します。

・ケース1

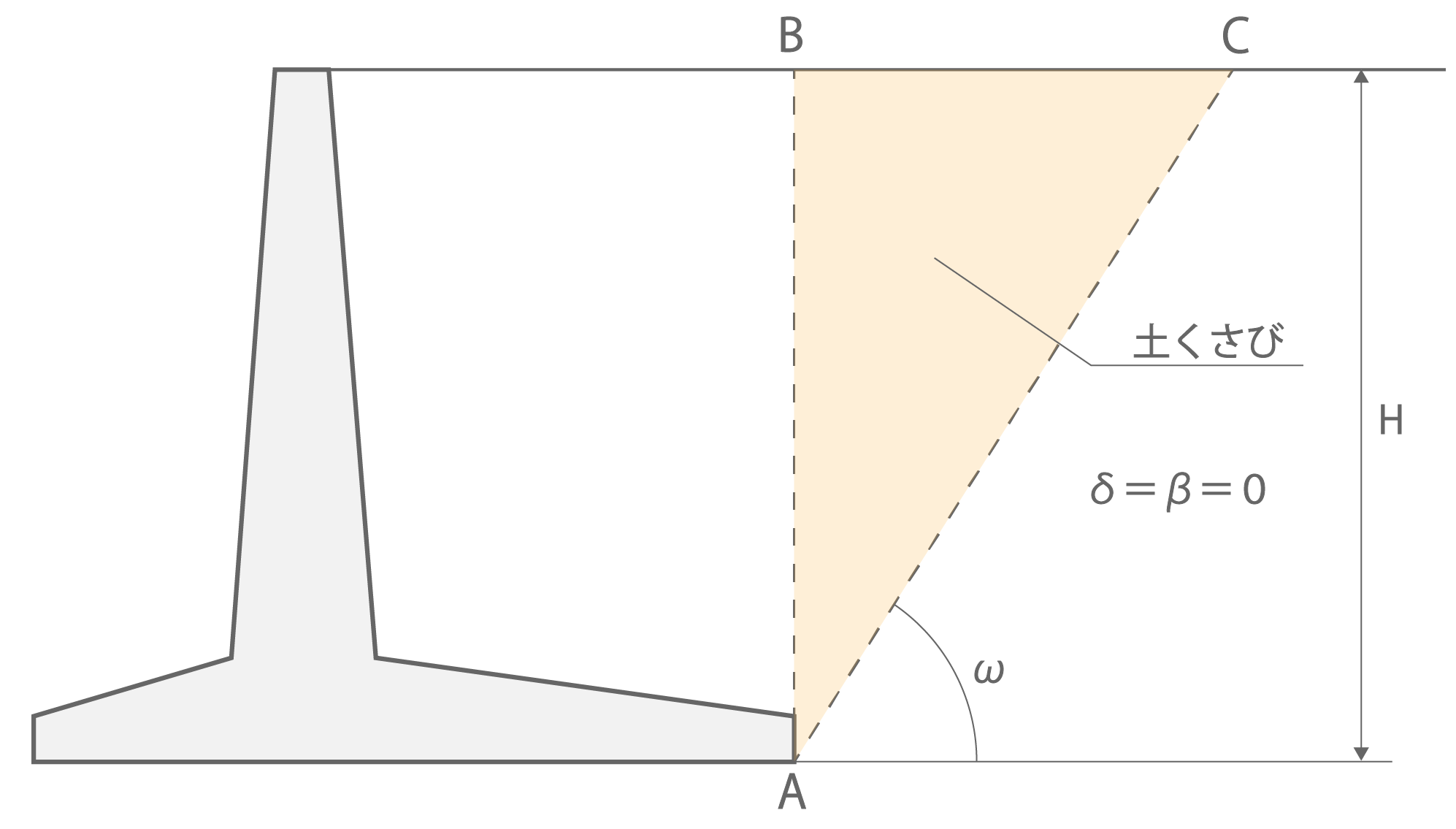
図1.4.a ケース1の土くさびの重量

\[ W = \frac{H^2}{2tanω}γ_{s} \]

・ケース2

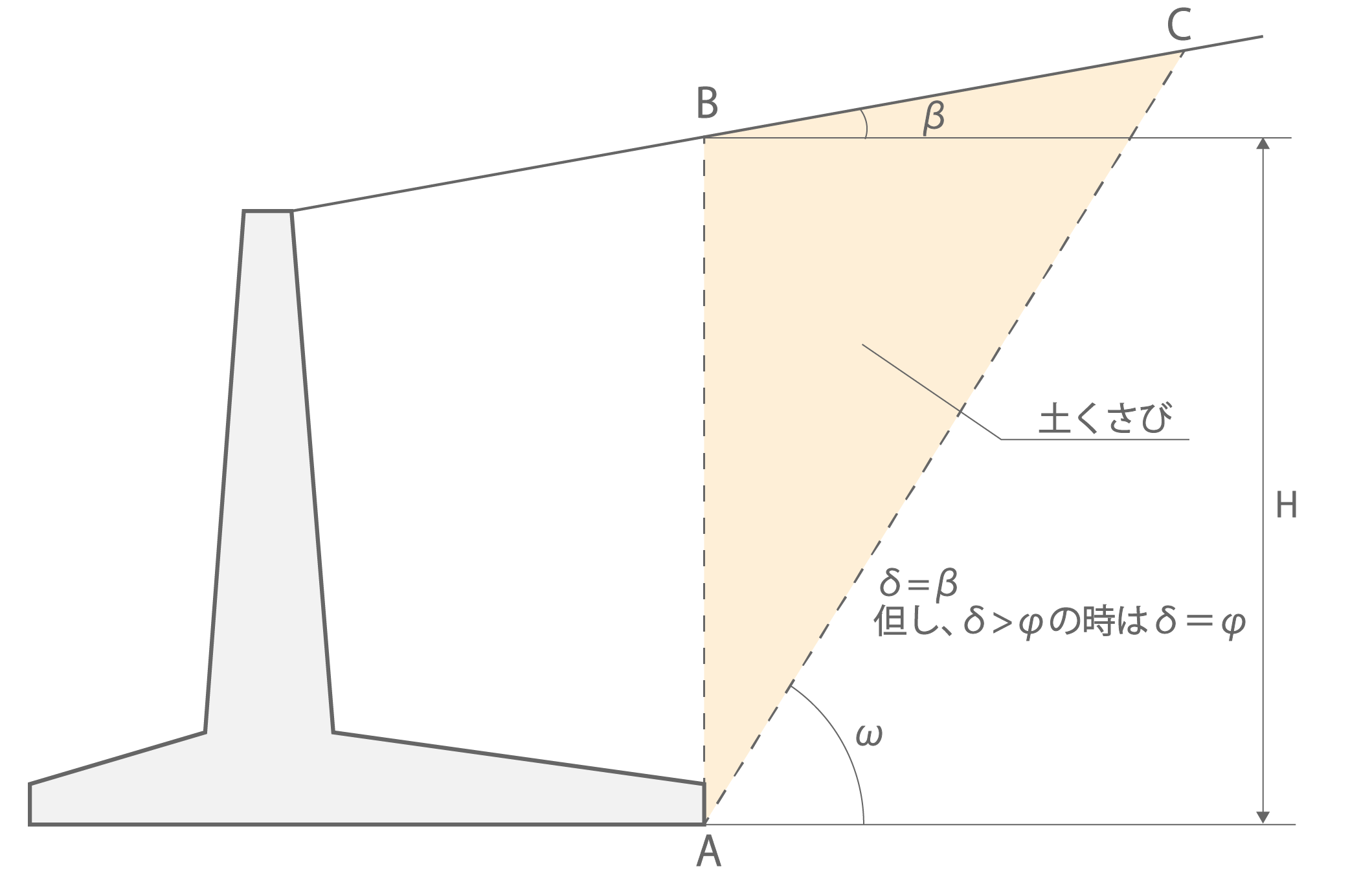
図1.4.b ケース2の土くさびの重量

\[ W = \frac{H^2}{2(tanω-tanβ)}γ_{s} \]

・ケース3

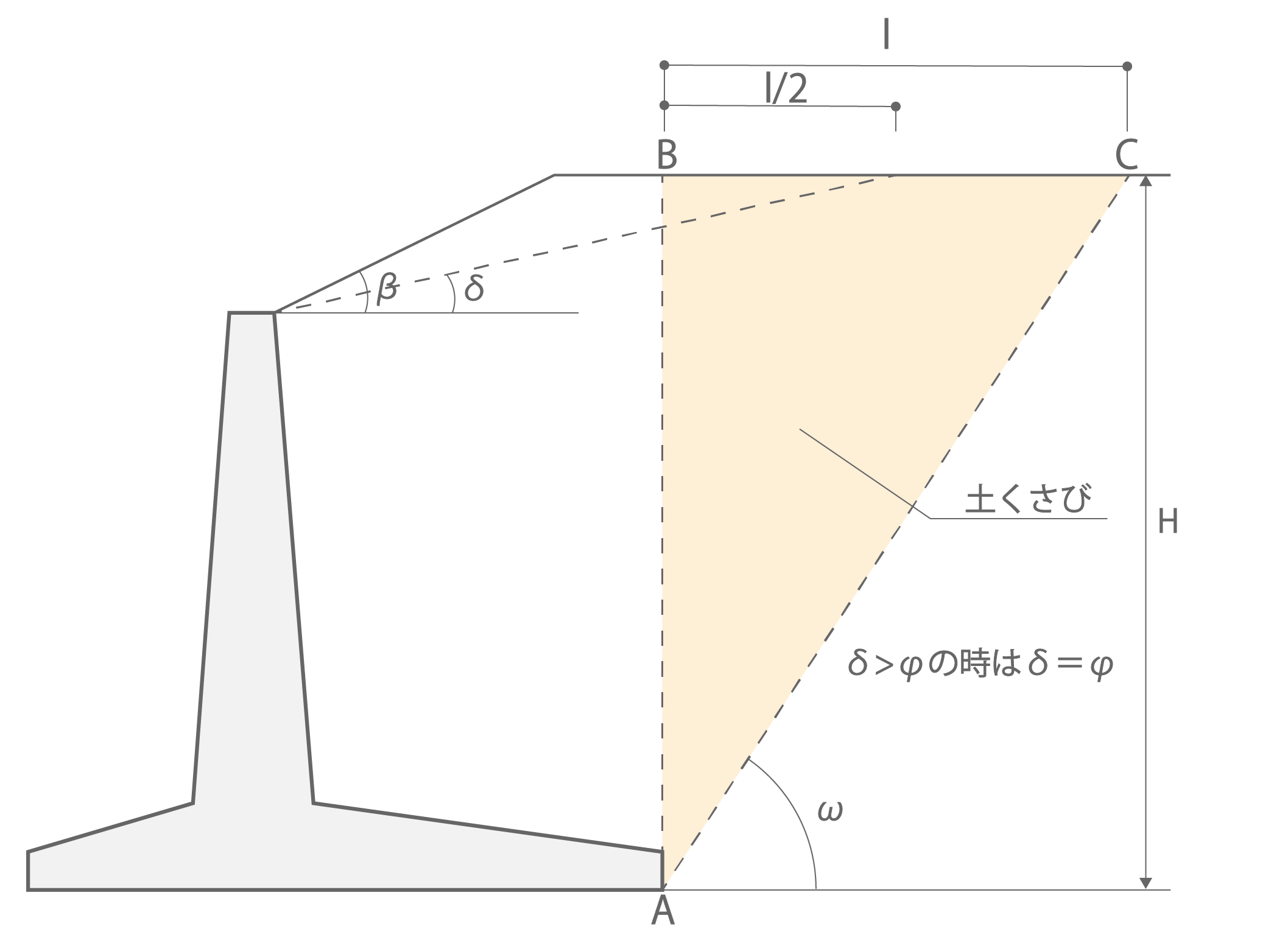
図1.4.c ケース3の土くさびの重量

\[ W = \frac{H^2}{2tanω}γ_{s} \]

・ケース4

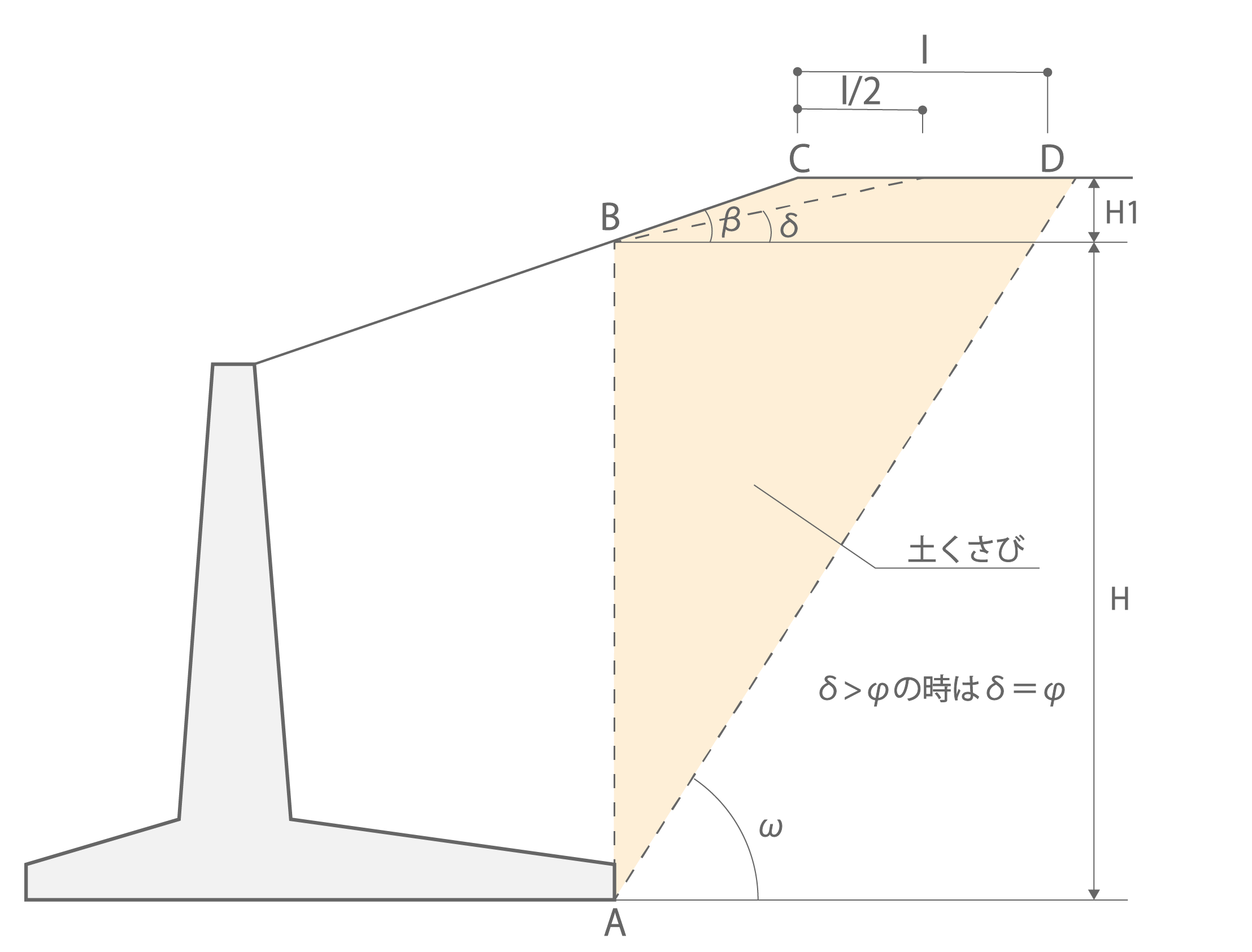
図1.4.d ケース4の土くさびの重量

\[ W = H^2\left\{\frac{1}{2tanω}\left(1+\frac{H_{1}}{H}\right)^2-\frac{1}{2tanβ}\left(\frac{H_{1}}{H}\right)^2\right\}γ_{s} \]
b) たて壁設計用

たて壁設計用の土くさびの重量はケース1～4のいづれかにより計算します。

・ケース1

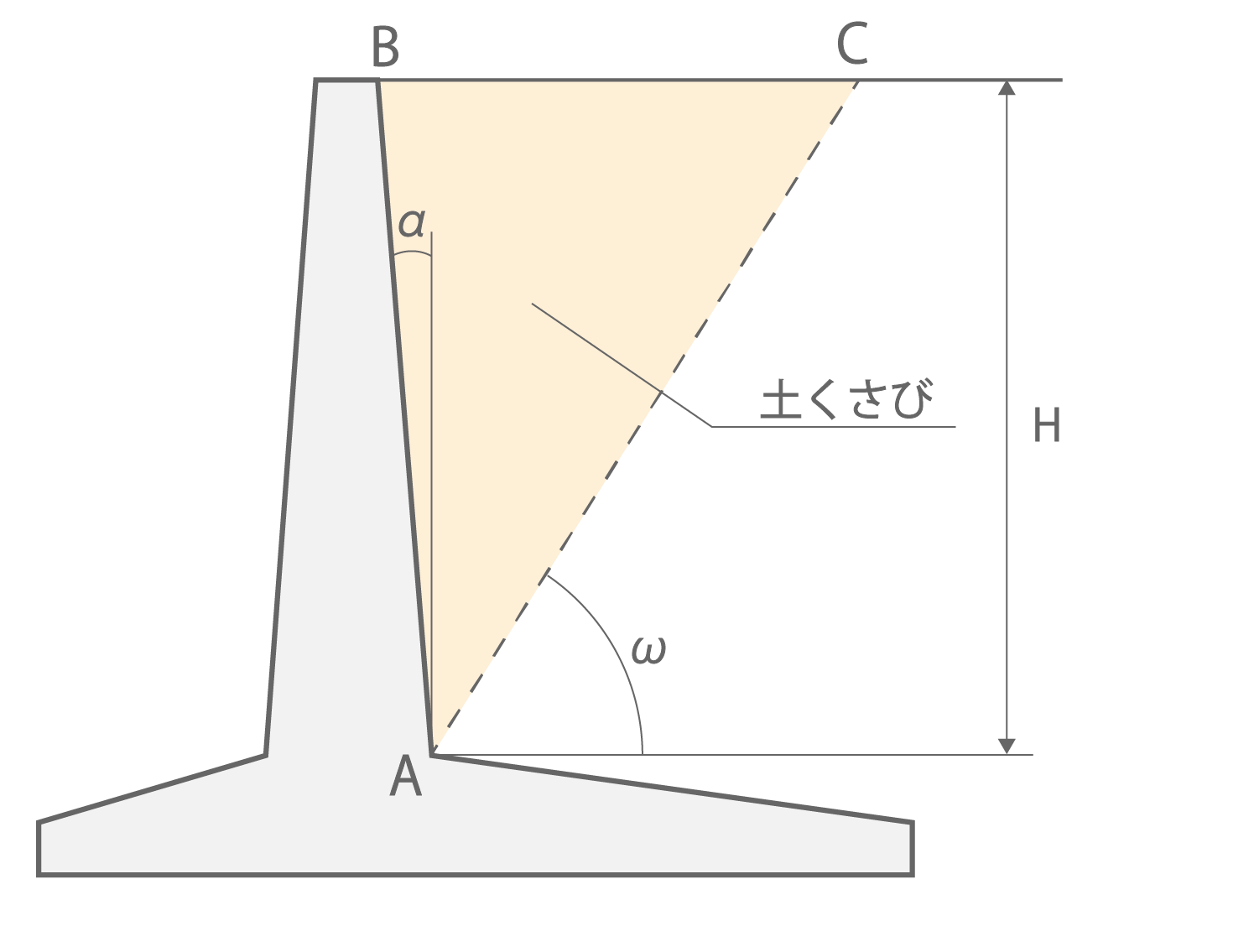
図1.5.a ケース1の土くさびの重量(たて壁用)

\[ W = \frac{1+tanωtanα}{2tanω}γ_s \]

・ケース2

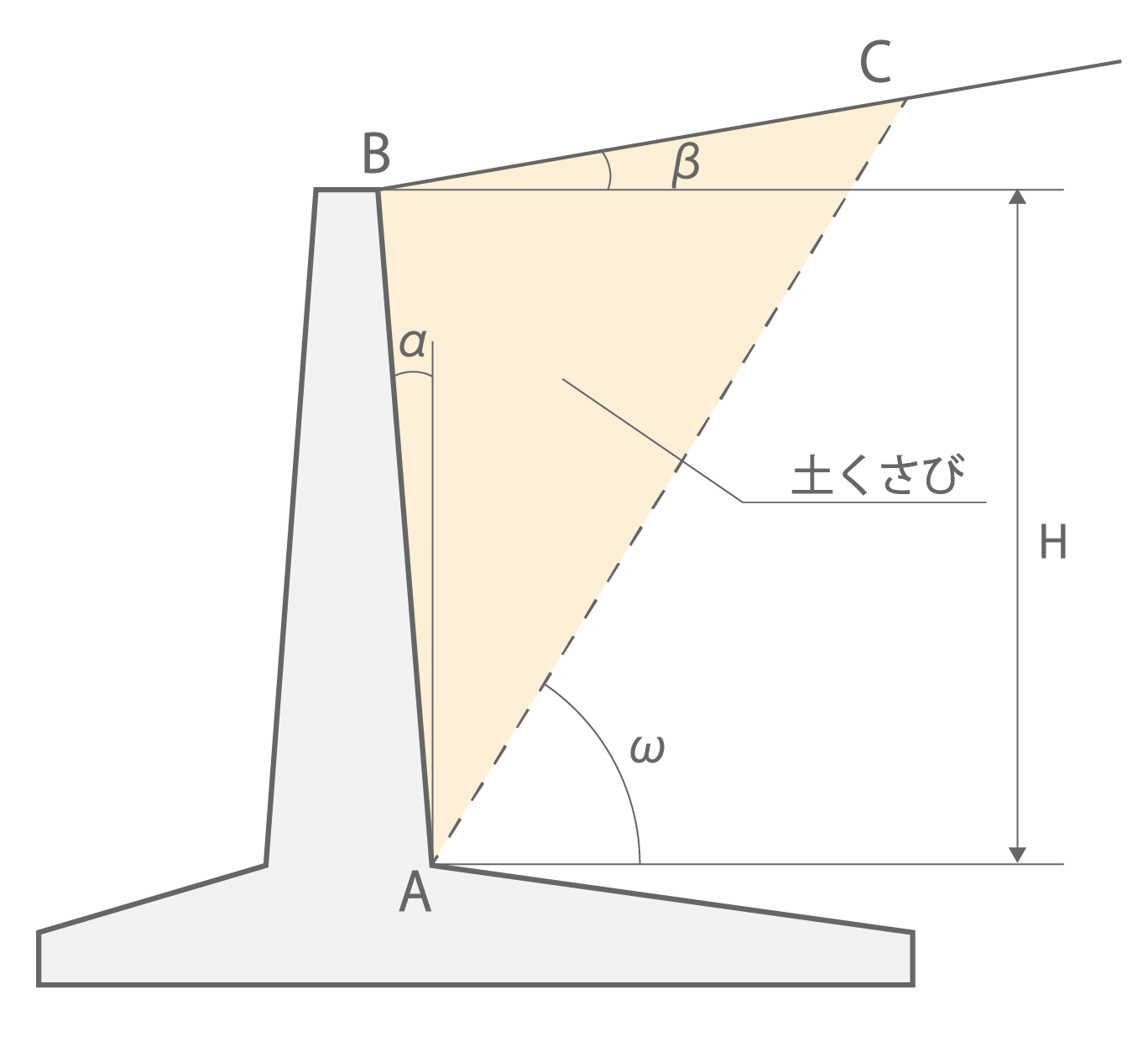
図1.5.b ケース2の土くさびの重量(たて壁用)

\[ W = \frac{\left(1+tanωtanα\right)\left(1+tanαtanβ\right)}{2\left(tanω-tanβ\right)}γ_{s} \]

・ケース3

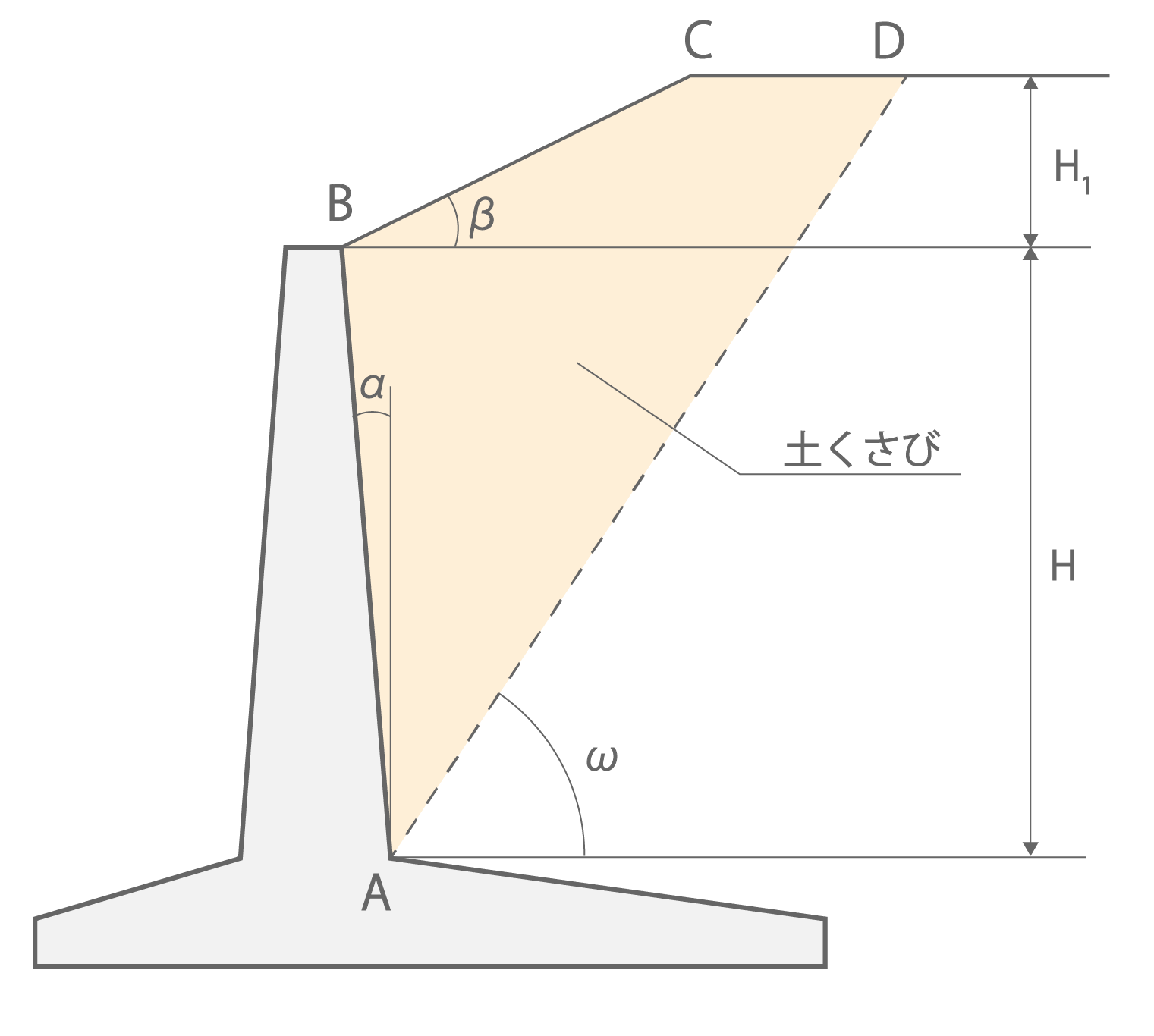
図1.5.c ケース3の土くさびの重量(たて壁用)

\[ W = H^2\left\{\left(tanα + \frac{1}{tanω}\right)\left(\frac{1}{2}+\frac{H_{1}}{H}\right)+\frac{1}{2}\left(\frac{1}{tanω}-\frac{1}{tanβ}\right)\left(\frac{H_1}{H}\right)^2\right\}γ_s \]

2. 擁壁の安定計算の方法

片持ち擁壁の安定計算では、外力に対して、「転倒」、「滑動」、「支持力」に対する安定性の確認を行います。

2.1. 転倒に対する検討

擁壁に作用する水平力により、底盤のつま先を中心として転倒させるモーメントが働きます。これに抵抗する方向に働くモーメントの大きさが必要な安全率以上であることを確認する。

a) 常時

常時の転倒に対する検討では、原点から荷重の合力の作用点までの距離dを式(2.1.2)により求め、dが底盤中央の1/3以内であることを確認します。

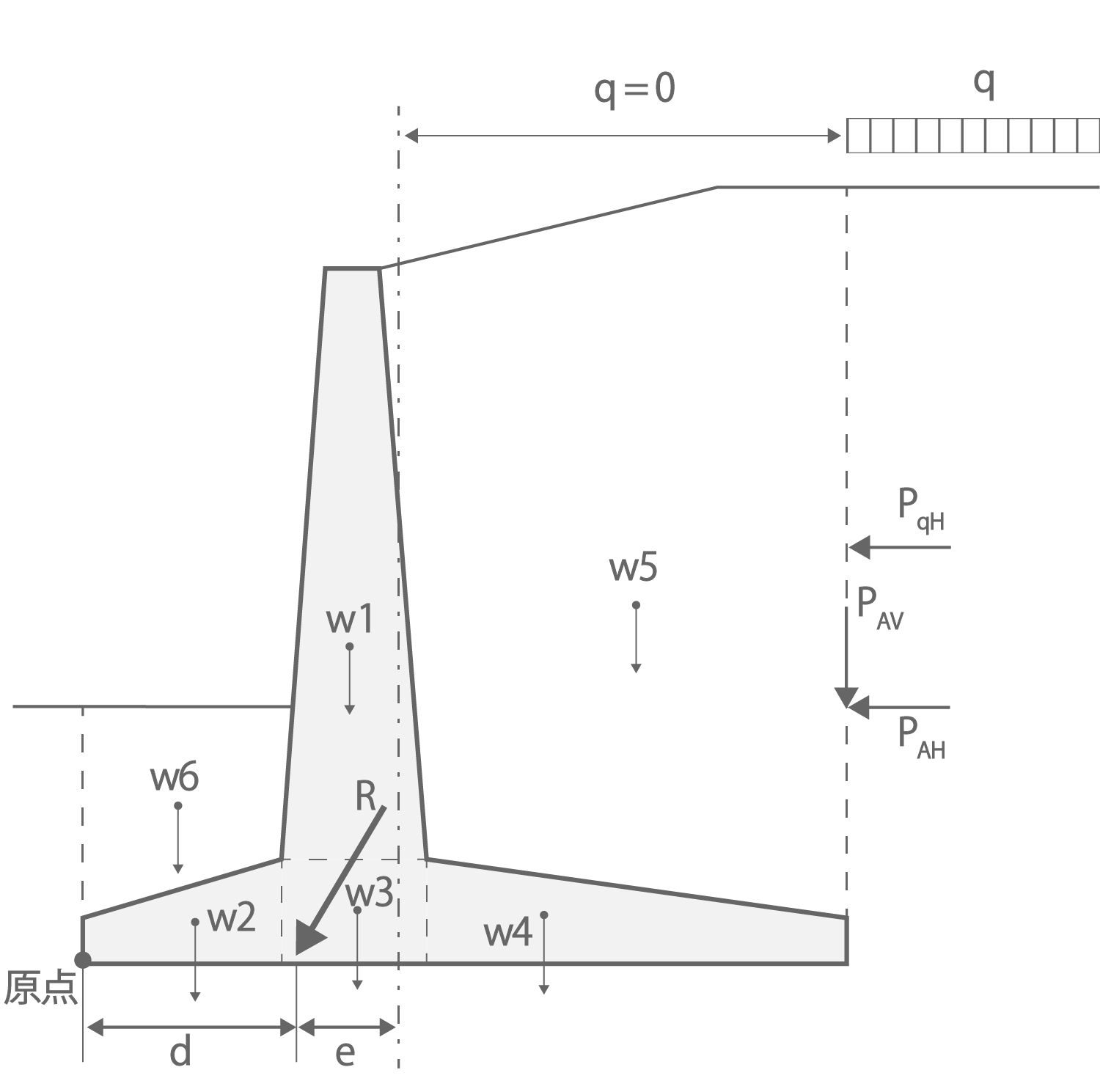
図2.1 原点まわりに作用する荷重

\[ d = \frac{M_{r} - M_{0}}{V}・・・・(2.1.1) \] \[ e = \frac{L_{W}}{2} - d ≦ \frac{L_{W}}{6}・・・・(2.1.2) \]

記号

Mr : 抵抗モーメント、式(2.1.3)によります。
\[ M_{r} = W・x_{wg} + P_{AV}・X_{ag}・・・・(2.1.3) \]

ここに

W : 土くさびの重量
Xwg : 原点と土くさびの重心との水平距離
PaV : 鉛直方向の土圧合力
Xag : 原点とPaVの作用点との水平距離
M0 : 転倒モーメント、式(2.1.4)によります。
\[ M_{0} = P_{AH}・y_{ag} + P_{qH}・y_{qg}・・・・(2.1.4) \]

ここに

PAH : 鉛直方向の土圧合力
yAg : 原点とPHの作用点との鉛直距離
PqH : 載荷重による土圧合力
yqg : 原点とPqHの作用点との鉛直距離
V : 鉛直荷重の合計、式(2.1.5)によります。
\[ V = W + P_{aV}・・・・(2.1.5) \]

記号は前出によります。

また、Mr/M0が指定したな安全率以上であることを確認します。デフォルトは1.5以上です。

b) 地震時

原点から荷重の合力の作用点までの距離dEを求め、dEが底盤中央の2/3以内であることを確認します。

\[ d_{E} = \frac{M_{rE} - M_{0E}}{V_{E}}・・・・(2.1.6) \] \[ e_{E} = \frac{L_{W}}{2} - d_{E} ≦ \frac{L_{W}}{3}・・・・(2.1.7) \]

記号

MrE : 抵抗モーメント、下式によります。
\[ M_{rE} = W・x_{wg} + P_{AVE}・X_{ag}・・・・(2.1.8) \]

ここに

W : 土、擁壁自重(W1～6)の合計
Xwg : 原点と土くさびの重心との水平距離
PAVE : 地震時鉛直方向の土圧合力
Xag : 原点とPaVEの作用点との水平距離
M0E : 転倒モーメント、下式によります。
\[ M_{0E} = P_{AHE}・y_{ag} + P_{qHE}・y_{qg} + W_{1～5}・k_{h}・y_{wg} + _{t}P_{H}・y_{tg}・・・・(2.1.9) \]

ここに

PAHE : 地震時鉛直方向の土圧合力
yag : 原点とPHの作用点との鉛直距離
PqHE : 地震時載荷重による土圧合力
yqg : 原点とPqHの作用点との鉛直距離
kh : 設計用水平震度
tPH : 擁壁頂部に作用する水平力
ytg : 原点から擁壁頂部までの鉛直距離
VE : 地震時鉛直荷重の合計、下式によります。
\[ V = W + P_{AVE}・・・・(2.1.10) \]

記号は前出によります。

また、Mr/M0が指定した安全率以上であることを確認します。デフォルトは1.0以上です。

2.2. 滑動に対する検討

滑動に対する検討では、水平力に対する、底盤下面と基礎地盤との摩擦力が指定した安全率以上であることを確認します。なお摩擦力の計算では載荷重は０として計算します。作用する荷重は図2.1によります

a) 常時
\[ F_{S} = \frac{底盤と地盤との間の摩擦力}{水平力}　= \frac{(W + P_{AV})μ}{P_{aH} + P_{qH}} > ユーザー指定の安全率・・・・(2.2.1) \]

記号

FS : 安全率
W : 擁壁および地盤の自重
μ : 摩擦係数
PAV : 鉛直方向の土圧合力
PaH : 水平方向の土圧合力
PqH : 水平方向の載荷重合力
b) 地震時
\[ F_{SE} = \frac{底盤と地盤との間の摩擦力}{水平力}　= \frac{(W + P_{AVE})μ}{P_{AHE} + P_{qHE} + _{t}P_{H}} > ユーザー指定の安全率・・・・(2.2.2) \]

記号

FSE : 安全率
PAVE : 地震時鉛直方向の土圧合力
PAHE : 地震時水平方向の土圧合力
PqHE : 地震時水平方向の載荷重合力
tPH : 擁壁頂部の水平力
その他の記号は前出によります。

2.3. 支持力に対する検討

支持力に対する検討では、底盤に作用する最大の地反力度がユーザー指定の安全率により低減した許容地耐力以下であることを確認します。底盤に作用する地反力度は下式により計算します。

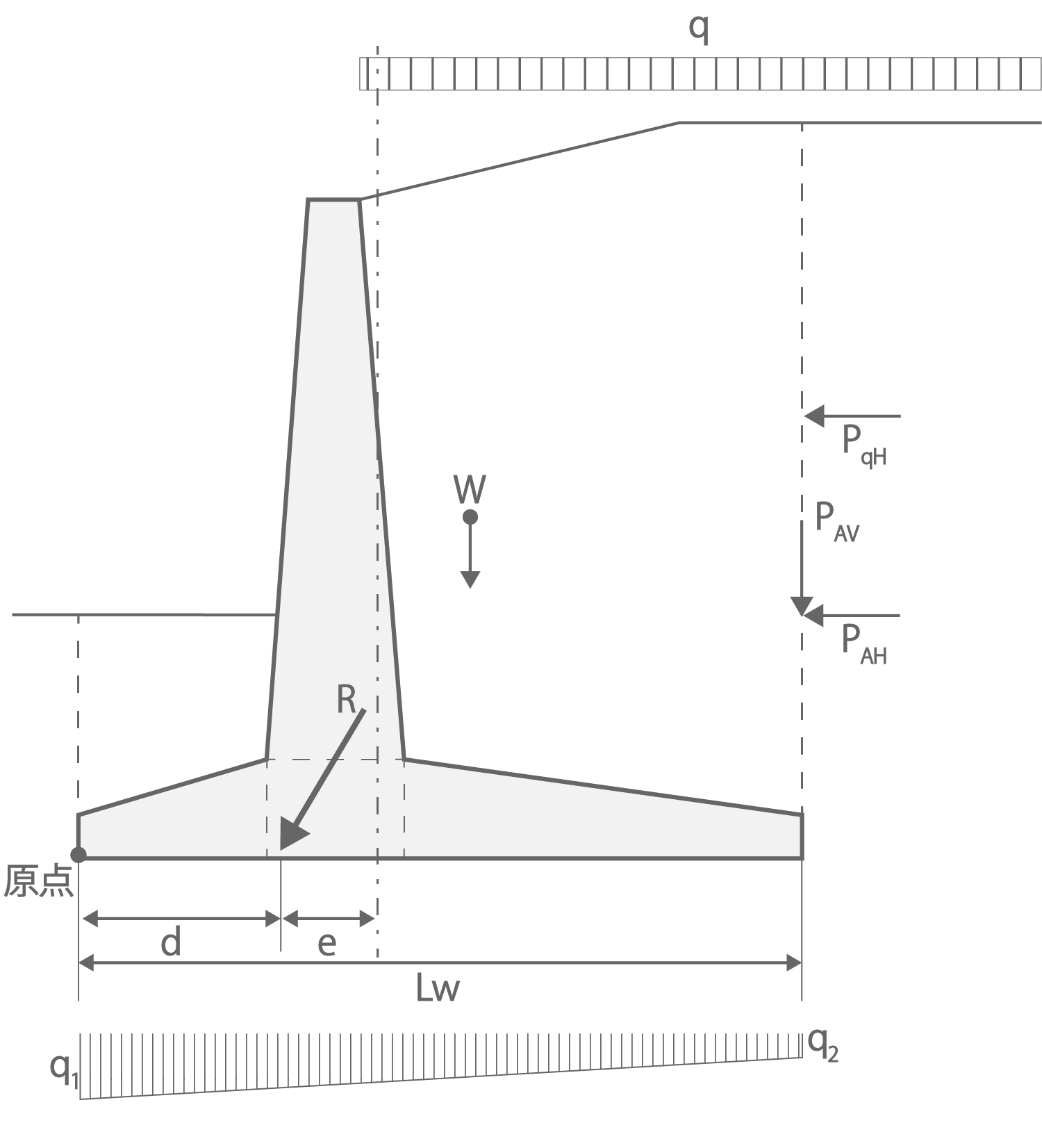
図2.2 支持力検討用の荷重

a) 常時
\[ q_{1} = \frac{W + P_{AV} + V_{q}}{B}\left(1+\frac{6e}{L_{W}}\right)・・・・(2.3.1) \] \[ q_{2} = \frac{W + P_{AV} + V_{q}}{B}\left(1-\frac{6e}{L_{W}}\right)・・・・(2.3.2) \]

q1,q2が以下を満足していることを確認します。

\[ q_{1}　or　q_{2} ≦ \frac{_{L}f_{e}}{安全率}・・・・(2.3.3) \]

記号

q1,q2 : 地盤反力度
W : 擁壁および地盤の自重
PAV : 鉛直方向の土圧合力
Vq : 鉛直方向の載荷重合力
LW : 底盤の全長
e : 合力の作用点の底盤中央からの偏心距離(2.1. 転倒に対する検討にて解説しています。)
Lfe : 長期許容地耐力
その他の記号は前出によります。
b) 地震時
\[ q_{1E} = \frac{W + P_{AVE} + V_{qE}}{B}\left(1+\frac{6e_{E}}{L_{W}}\right)・・・・(2.3.4) \] \[ q_{2E} = \frac{W + P_{AVE} + V_{qE}}{B}\left(1-\frac{6e_{E}}{L_{W}}\right)・・・・(2.3.5) \]

q1E,q2Eが以下を満足していることを確認します。

\[ q_{1E}　or　q_{2E} ≦ \frac{_{E}f_{e}}{安全率}・・・・(2.3.6) \]

記号

q1E,q2E : 地震時地盤反力度
PAVE : 地震時鉛直方向の土圧合力
VqE : 地震時鉛直方向の載荷重合力
eE : 地震時合力の作用点の底盤中央からの偏心距離(2.1. 転倒に対する検討にて解説しています。)
Efe : 地震時許容地耐力

3. 擁壁の断面算定

片持ち擁壁の断面算定では、外力に対してたて壁、底盤にかかる応力が許容応力度以下であることを確認します。

3.1. たて壁の設計

3.1.1 設計用応力

たて壁に作用する外力は図3.1によります。曲げ、せん断応力は式(3.1.1)～(3.1.2)によります。

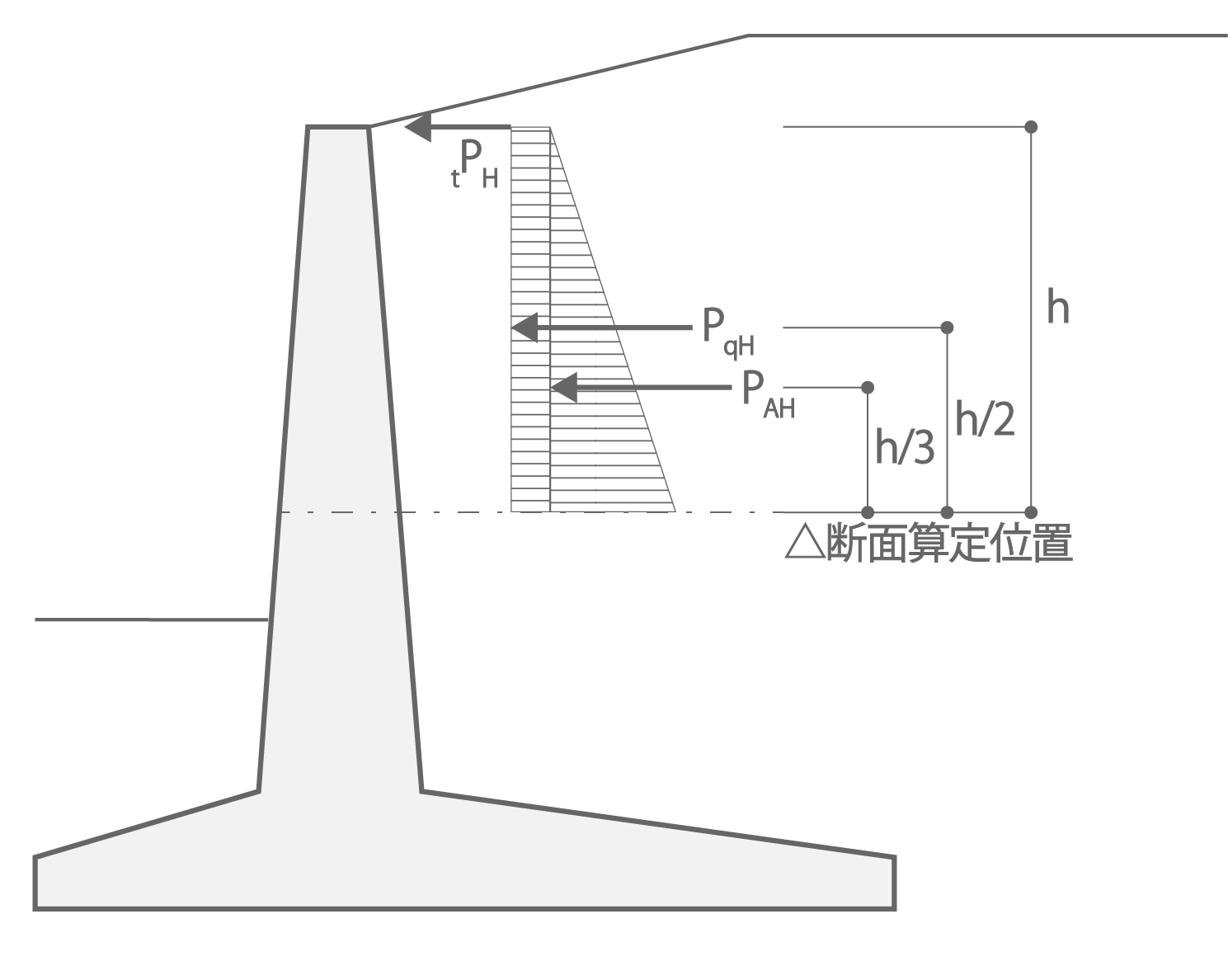
図3.1 たて壁に作用する外力

a) 常時
\[ \begin{aligned} M_{hL} = P_{AH}・\frac{h}{3} + P_{qH}・\frac{h}{2}・・・・(3.1.1)\\ Q_{hL} = P_{AH} + P_{qH}・・・・(3.1.2) \end{aligned} \]

記号

MhL : 擁壁天端からhの位置の常時たて壁設計用曲げモーメント
QhL : 擁壁天端からhの位置の常時たて壁設計用せん断力
PAH : たて壁設計用土圧水平力の合力(=γs・KA・h2/2)
PqH : たて壁設計用載荷重水平力の合力(=qL・KA・h)
h : 擁壁天端から断面算定位置までの鉛直距離
KA : 常時土圧係数
γs : 土の単位体積重量
qL : 常時の単位面積あたりの載荷重
b) 地震時
\[ \begin{aligned} M_{hE} = P_{AHE}・\frac{h}{3} + P_{qHE}・\frac{h}{2} + _{t}P_{H}・h・・・・(3.1.3)\\ Q_{hE} = P_{AHE} + P_{qHE} + _{t}P_{H}・・・・(3.1.4) \end{aligned} \]
MhE : 擁壁天端からhの位置のたて地震時壁設計用曲げモーメント
QhE/sub> : 擁壁天端からhの位置の地震時たて壁設計用せん断力
PAHE : 地震時たて壁設計用土圧水平力の合力(=γs・KAE・h2/2)
PqHE : 地震時たて壁設計用載荷重水平力の合力(=qE・KAE・h)
KAE : 地震時土圧係数
qE : 地震時の単位面積あたりの載荷重
その他の記号は前出によります。

3.1.2 断面算定

3.1.1で求めた設計用応力が許容曲げ耐力Maおよび、Qa未満であることを確認します。許容耐力は下記によります。

a) 常時
\[ \begin{aligned} M_{aL} = a_{t}・f_{tL}・j・・・・(3.1.5)\\ Q_{aL} = f_{sL}・j・・・・(3.1.6) \end{aligned} \]

記号

MaL : 幅1mあたりのたて壁長期許容曲げ応力
QAL : 幅1mあたりのたて壁の長期許容せん断力
at : たて壁1m当たりの引張鉄筋断面積の合計
ftL : 引張鉄筋の長期許容引張力
j : 応力中心間距離(=7d/8)
fsAL : コンクリートの長期許容せん断力
b) 地震時
\[ \begin{aligned} M_{aE} = a_{t}・f_{tE}・j・・・・(3.1.7)\\ Q_{aE} = f_{sE}・j・・・・(3.1.8) \end{aligned} \]

記号

MaE : 幅1mあたりのたて壁短期許容曲げ応力
QAE : 幅1mあたりのたて壁の短期許容せん断力
ftE : 引張鉄筋の短期許容引張力
fsE : コンクリートの短期許容せん断力

3.2. 底盤の設計

3.2.1 設計用応力

底盤に作用する応力は図3.2に示すように、地反力による曲げ応力Mqおよびせん断力Qqと、底盤上部の土および自重による曲げ応力Mwおよびせん断力QWの差を求めます。

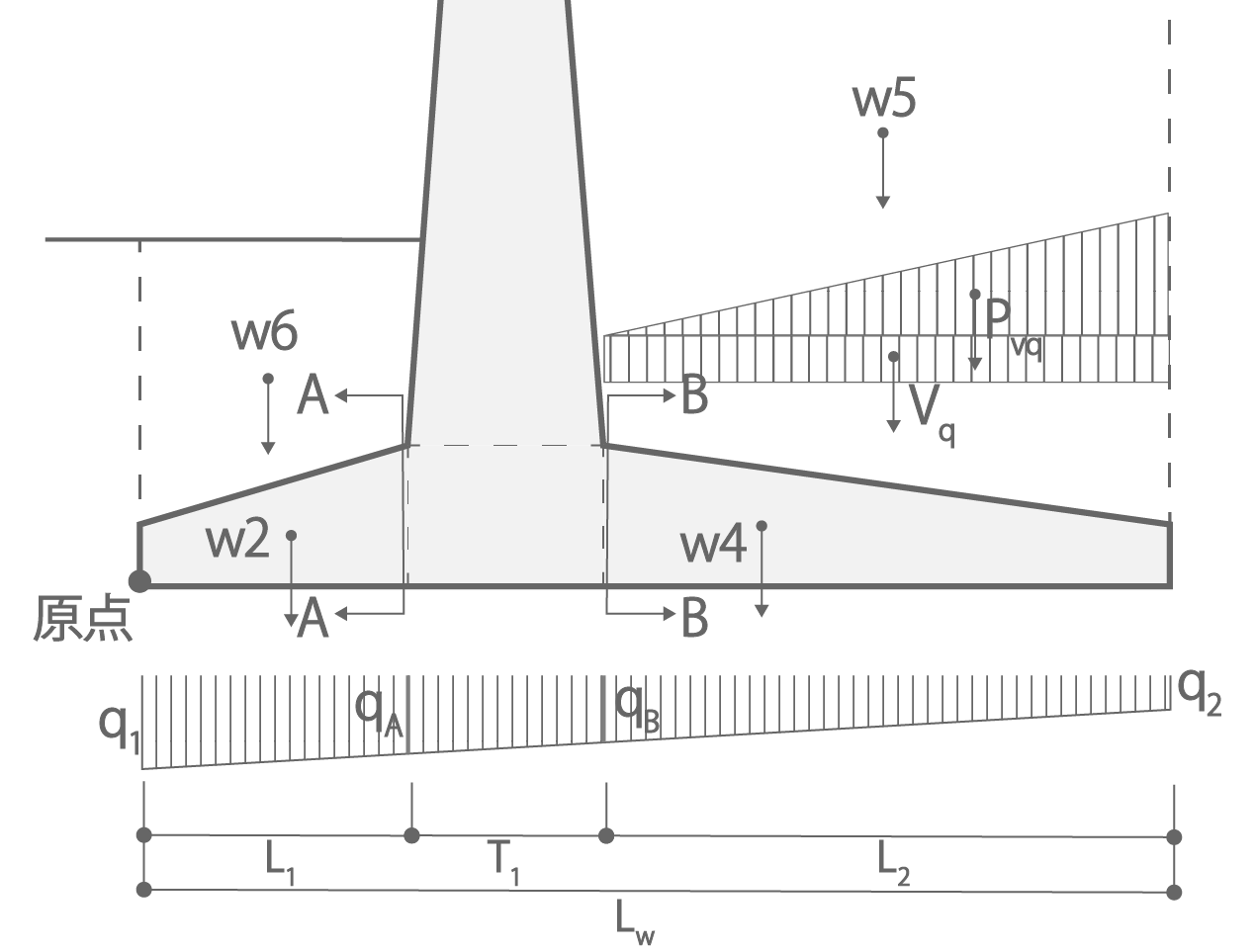
図3.2 底盤に作用する外力

\[ \begin{aligned} M = M_{q} - M_{W}・・・・(3.2.1)\\ Q = Q_{q} - Q_{W}・・・・(3.2.2) \end{aligned} \]

記号

Mq : 地反力度による曲げ応力
MW : 上載土、基礎自重による曲げ応力
Qq : 地反力度によるせん断力
QW : 上載土、基礎自重によるせん断力
a) 常時
i) A-A断面
\[ \begin{aligned} M_{q} &= \frac{q_{1} + q_{A}}{6}・L_{1}^{2}・・・・(3.2.3) \\ M_{W} &= W_{2}・X_{w2} + W_{5}・X_{w5} ・・・・(3.2.4)\\ Q_{q} &= \frac{q_{1} + q_{A}}{2}・L_{1}・・・・(3.2.5) \\ Q_{W} &= W_{2} + W_{5}・・・・(3.2.6) \end{aligned} \]

記号

qA : A-A断面における地反力度
\[q_{A} = q_{2} + (q_{1} - q_{2})・\frac{T_{1}+L_{2}}{L_{W}}\]
W2 : 擁壁つま先部分の自重合力
W5 : 擁壁つま先部分の上載土自重合力
XW2 : W2が作用する位置からA-A断面までの距離
XW5 : W5が作用する位置からA-A断面までの距離
ii) B-B断面
\[ \begin{aligned} M_{q} = \frac{2q_{2} + q_{B}}{6}・L_{2}^{2}・・・・(3.2.7) \\ M_{W} = W_{4}・X_{w4} + W_{6}・X_{w6} + P_{ALV}・X_{ga} + V_{qL}・X_{gq}・・・・(3.2.8) \\ Q_{q} = \frac{q_{2} + q_{B}}{2}・L_{2}・・・・(3.17)\\ Q_{W} = W_{4} + W_{6} + P_{ALV} + P_{qLV}・・・・(3.2.9) \end{aligned} \]

記号

qB : B-B断面における地反力度
\[q_{B} = q_{2} + (q_{1} - q_{2})・\frac{L_{2}}{L_{W}}\]
W4 : 擁壁かかと部分の自重合力
W6 : 擁壁かかと部分の上載土自重合力
XW4 : W4が作用する位置からB-B断面までの距離
XW6 : W6が作用する位置からB-B断面までの距離
PALV : 土圧合力の鉛直成分
Xga : 土圧合力の鉛直成分が作用する位置からB-B断面までの距離(=2・L2/3)
VqL : 上載荷重の合力
Xgq : 上載荷重の合力の作用する位置
b) 地震時
i) A-A断面
\[ \begin{aligned} M_{qE} &= \frac{q_{1E} + q_{AE}}{6}・L_{1}^{2}・・・・(3.2.10) \\ M_{WE} &= W_{2}・X_{w2} + W_{5}・X_{w5} ・・・・(3.2.11)\\ Q_{qE} &= \frac{q_{1E} + q_{AE}}{2}・L_{1}・・・・(3.2.12) \\ Q_{WE} &= W_{2} + W_{5}・・・・(3.22) \end{aligned} \]

記号

qAE : 地震時のA-A断面における地反力度
\[q_{AE} = q_{2E} + (q_{1E} - q_{2E})・\frac{T_{1}+L_{2}}{L_{W}}\]
その他の記号は前出によります。
ii) B-B断面
\[ \begin{aligned} M_{qE} = \frac{2q_{2E} + q_{BE}}{6}・L_{2}^{2}・・・・(3.2.13) \\ M_{WE} = W_{4}・X_{w4} + W_{6}・X_{w6} + P_{AEV}・X_{ga} + V_{qE}・X_{gq}・・・・(3.2.14) \\ Q_{qE} = \frac{q_{2} + q_{B}}{2}・L_{2}・・・・(3.2.15)\\ Q_{WE} = W_{4} + W_{6} + P_{AEV} + P_{qEV}・・・・(3.2.16) \end{aligned} \]

記号

qBE : 地震時のB-B断面における地反力度
\[q_{BE} = q_{2E} + (q_{1E} - q_{2E})・\frac{L_{2}}{L_{W}}\]
PAEV : 地震時の土圧合力の鉛直成分
VqE : 地震時の上載荷重の合力

3.2.2 断面算定

3.2.1で求めた設計用応力が許容曲げ耐力Maおよび、Qa未満であることを確認します。許容耐力の計算方法は「3.1.2 断面算定」によります。

comming soon

1) ぎょうせい、宅地防災マニュアルの解説、2022.3

2) 日本道路協会、道路土工 擁壁工指針、2022.6

3) (社)日本建築学会、鉄筋コンクリート構造計算基準・同解説,2018.12

4) (社)日本建築学会、建築基礎構造設計指針 2010.12

5) 全国官報販売協同組合、2020年版 建築物構造関係技術基準解説書 2022.11

記号の解説

記号の解説

記号の解説

記号の解説

記号の解説

記号の解説

記号の解説

記号の解説